Core Components of CH
Adding Shortcuts
To reiterate: when contracting a node v, we consider the set of all vertices with edges incoming to v as U, and the set of all vertices with incoming edges from v as W.
For a node u in U and a vertex v in V, we only add a shortcut edge uw if the path <uvw> is the shortest path from u to w.
A straightforward approach
A straightforward way to determine which shortcuts are needed is to run a series of local shortest-path searches from every node u in U with v excluded. If we reach a node w in W with a distance less than w(u, v) + w(v, w), then we’ve just found a path witnessing that <uvw> is not the best way to get from u to w.
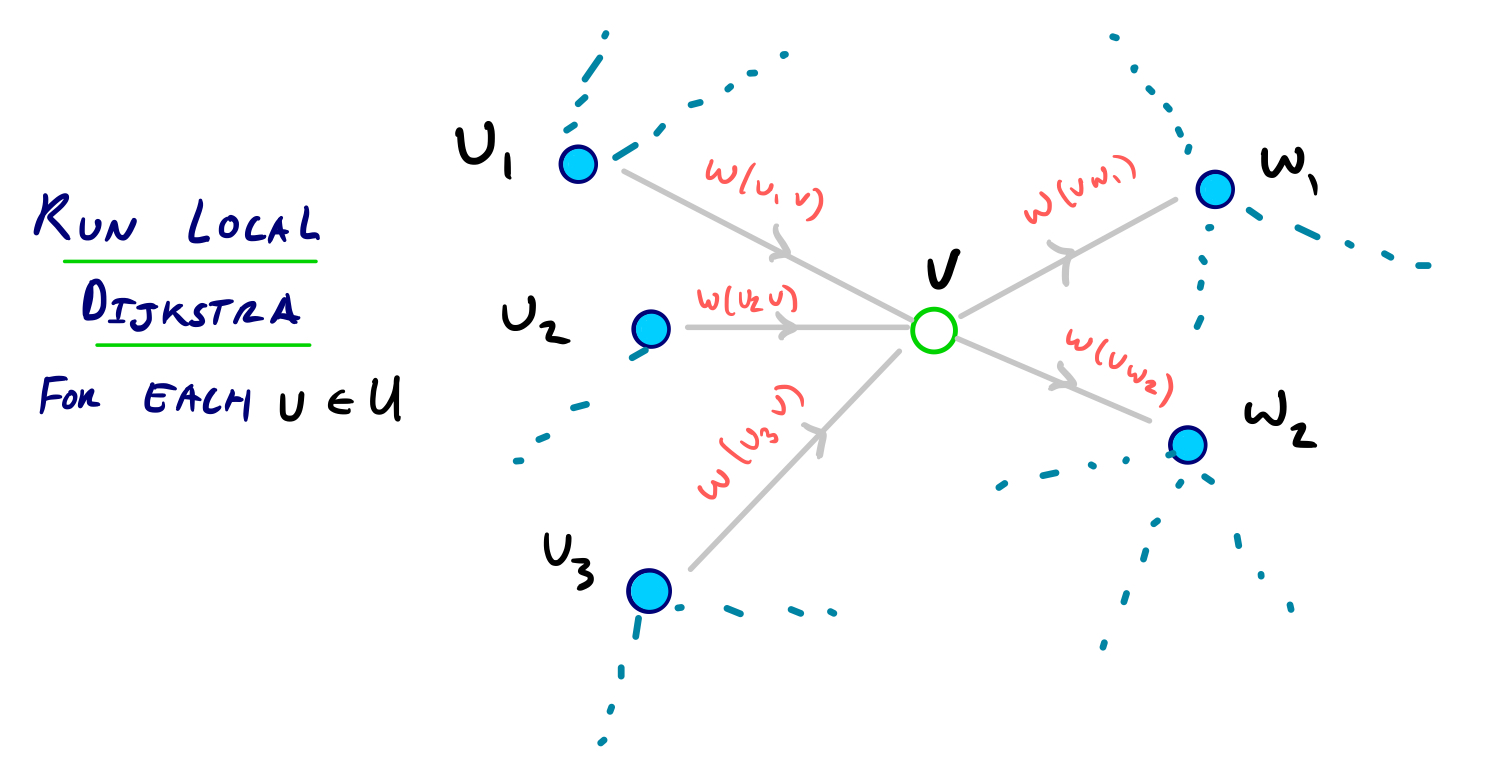
On the other hand, if <uvw> is the unique shortest path from u to w and moreover is the the only path from u to w, our local search won’t terminate since we’re considering the subgraph that excludes v.
So we can do the following for every u in U:
For every node w in W, compute Pw as the cost from u to w through v, which is the sum of the edge weights w(u, v) + w(v, w).
Then Pmax is the maximum Pw over all w in W.
Perform a standard Dijkstra’s shortest-path search from u on the subgraph excluding v.
Once a node is settled with a shortest-path score greater than Pmax, we stop.
Then for each w, if dist(u, w) > Pw we add a shortcut edge uw with weight Pw.
If this condition doesn’t hold, no shortcut is added.
Correctness
We stop this local search once we settle a node whose shortest path score is greater than Pmax. So, for a given node u in U, if there is a shortest path to some w in W, then the length of that path is less than Pw, and therefore less than or equal to Pmax. So the local search from u will not have stopped before finding the path and updating dist(u, w). Consider this example:
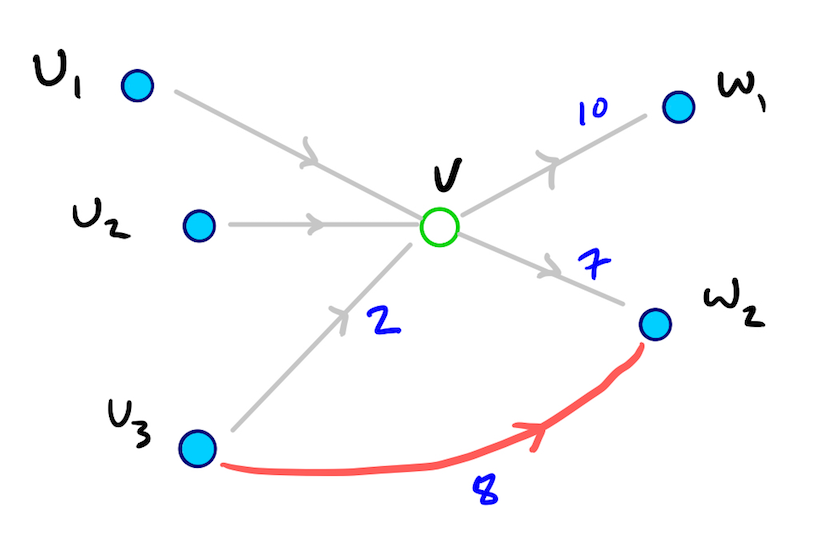
Here, when running a local Dijkstra search from u3, the value of Pmax is 12, and so the red edge representing the shortest path from u3 to w2 is relaxed before the local search halts. So in this case, no shortcut edge is added between u3 and w2
How Expensive are these Local Searches?
Running all of the local Dijkstra searches to contract a node can be expensive. For example, if Pmax is relatively large, it could take a while to settle a node whose shortest path score is greater than Pmax.
[9] and [8] provide a few heuristics to limit the search space during these local Dijkstra iterations. For example, we could put a limit on the number of nodes settled during a local search. If we reach this threshold before reaching a node whose shortest path score is greater than Pmax, we stop.
This could result in shortcut edges that aren’t actually needed, meaning that <uvw> is not the shortest path from u to w, but we added a shortcut uw anyways.
However, because shortcuts preserve shortest path structure, adding redundant shortcut edges doesn’t harm the correctness of queries. They do, however, contribute to the density of the final overlay graph, and so too many unnecessary shortcut edges can slow down queries.
So if limiting the search space size during these local Dijkstra rounds saves significant amounts of time during this preprocess stage, and the number of unnecessarily added shortcuts doesn’t substantially hurt query times, using an inexact heuristic could be beneficial.
This is a tradeoff that actual implementations take advantage of, but using the straightforward method we described above still gives adequate performance, both in the contraction stage and also in the query stage ([3]).
But as we said, unnecessary shortcuts don’t affect the correctness of queries, as long as every shortcut that is required gets added. And in general, given that the average degree of nodes in road networks is 2.5, we expect each local search to take constant time, meaning linear time over all nodes.
So now we actually look at the modified bidirectional query that is used following the successive contraction of all nodes.