CH Warmups
Bidirectional Dijkstra
Initially, we said that when using Dijkstra’s algorithm to perform a point-to-point query, we could achieve some pratical speedup by halting the search once our target node is settled.
We now introduce a bidirectional variant of Dijkstra’s algorithm that attempts to further reduce the number of nodes settled during a query.
Bidirectional Overview
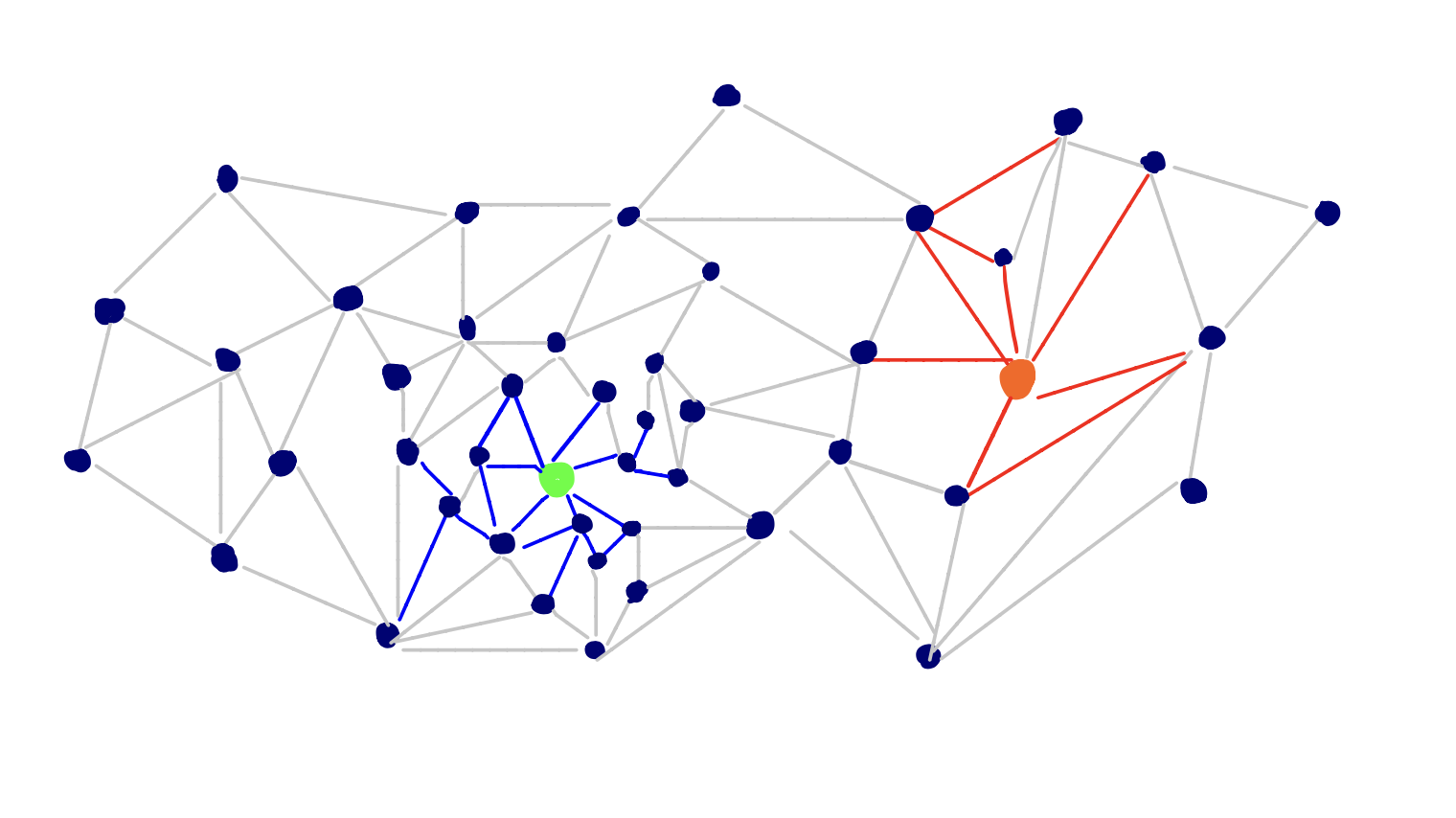
Rather than only run a Dijkstra query that settles nodes outward from the source, we simultaneoulsy run Dijkstra’s algorithm forward from the source and backward from the target.
We can halt the process after we settle a node in the forward search that was already settled in the backward search, or vice versa. This means the two searches have “met”. The node settled by both searches is not necessarily on the shortest path, but at this point, all nodes on the actual shortest path will already have been settled (we can prove this further below).
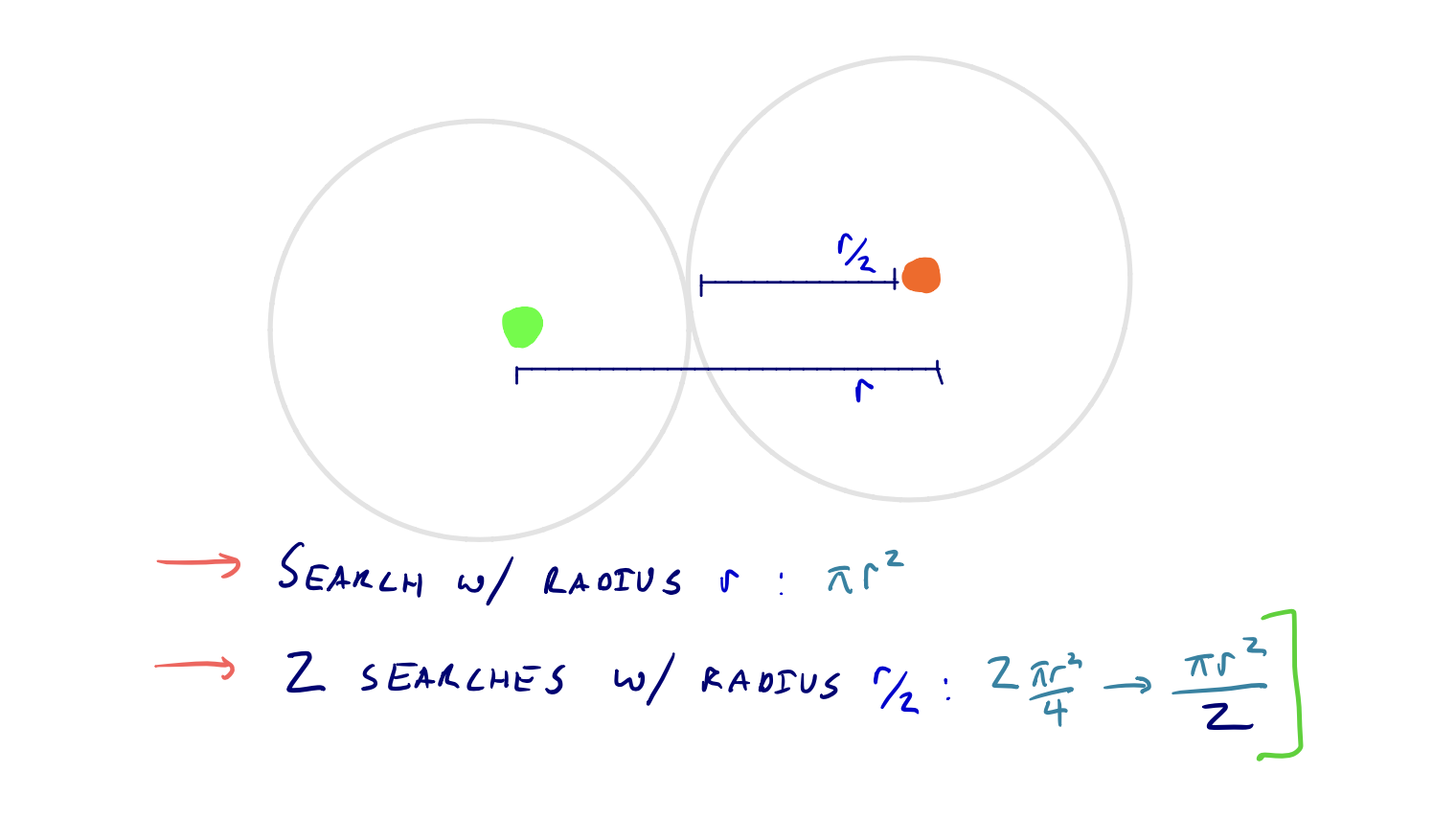
What does this achieve? As seen in the third slide, we can ideally reduce our search space by a factor of two. This isn’t guaranteed, but in practice ([2]), the number of nodes settled in a bidirectional query is about half the number of nodes settled in a standard Dijkstra query.
A two-times speedup is a good start, but with no other modifications, this would still require millions of nodes to be settled during queries on large road network graphs. However, contraction hierarchies utilizes a modified version of this bidirectional search, so it does offer a good foundation.
We offer some more details and a proof of correctness:
Bidirectional Details
To run two “simultaneous” rounds of Dijkstra’s algorithm, we maintain two priority queues and at each iteration either settle a node in the forward search, or settle a node in the backward search.
Note that the backward search starting at the target node considers the transpose of the graph, where all edge directions are flipped.
At each iteration, we compare the minimum node of the two priority queues, and we proceed with a round of Dijkstra in the priority queue with the smaller node.
We mark nodes that have already been settled by one of the searches, and when we settle a node that’s already been marked, our algorithm halts.
What’s the Shortest Path?
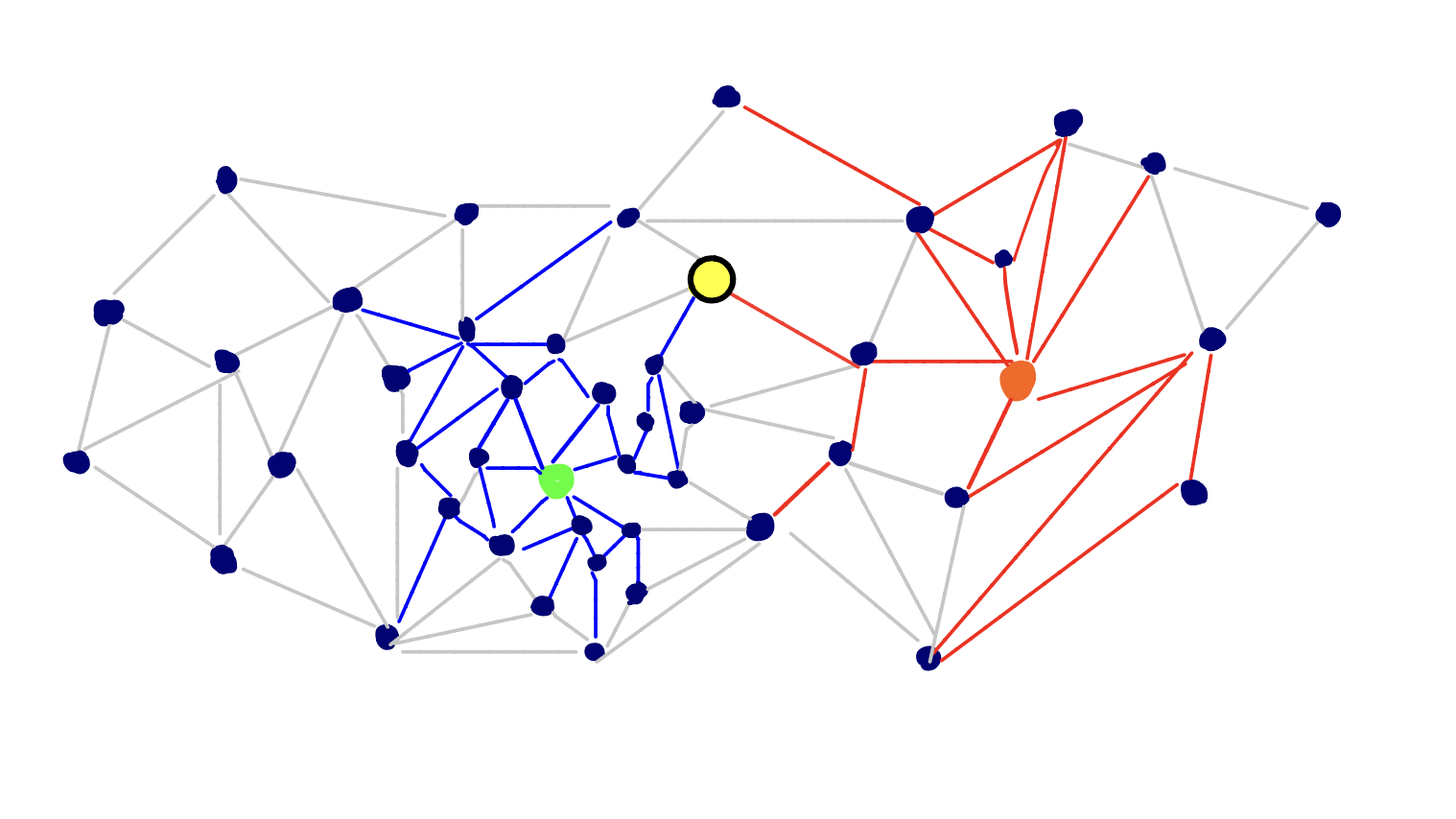
Is the node settled by both searches on the shortest path? It could be, but not always. Consider this counter example:
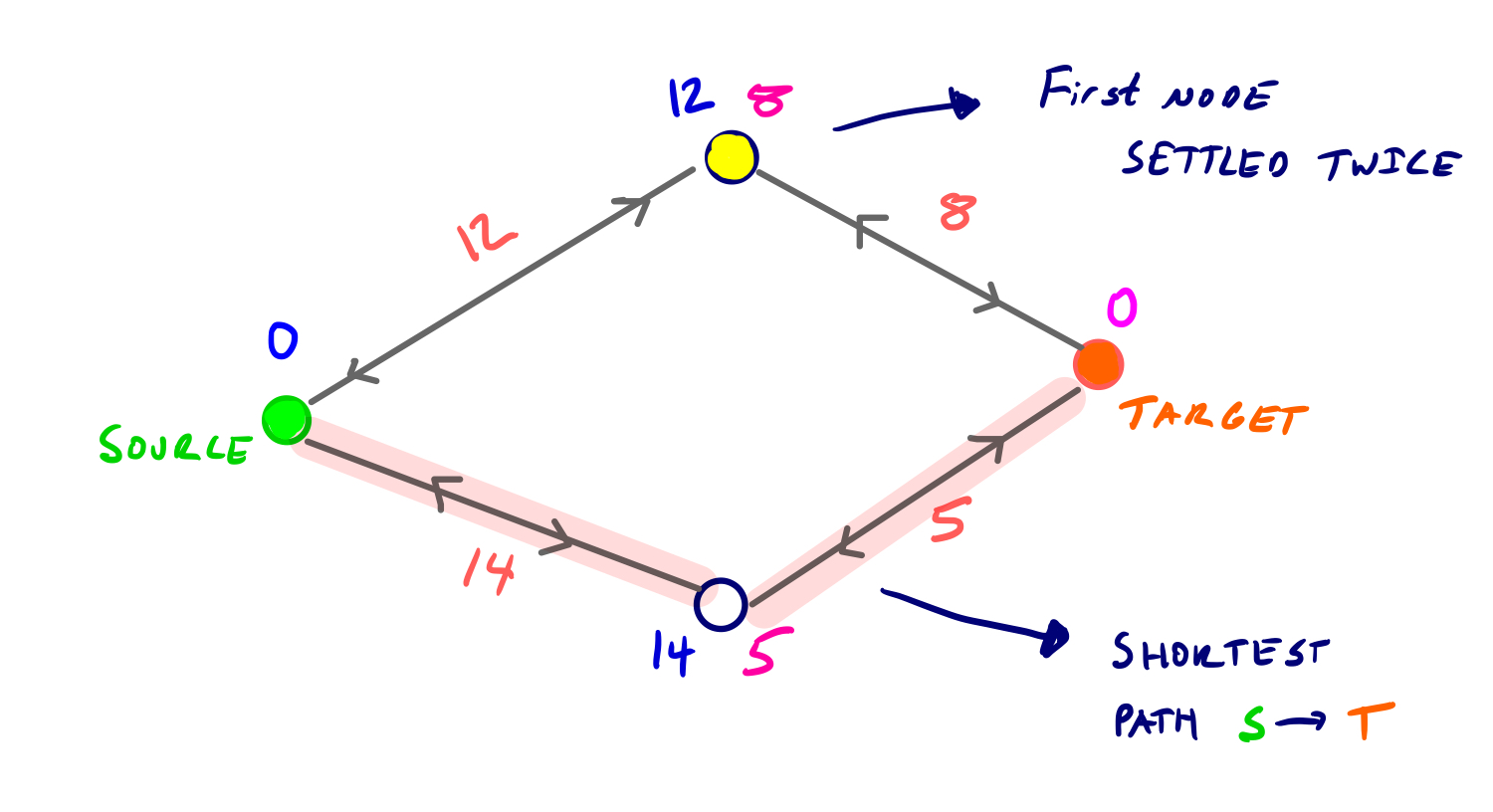
At each iteration we settle the smaller of the minimum nodes in the two priority queues. So we first settled the yellow node in the reverse search, then the bottom node in the reverse search, and then the yellow node again in the forward search.
So our search would halt since we’ve settled a node in both searches now, but the actual shortest path goes along the pink shaded edges.
The actual shortest path, then, is defined as:
For all u reached by both searches, dist(s, t) = min{dist(s,u) + dist(t,u)}
This means that we look at all vertices with finite shortest path scores from both s and t, and take the minimum sum of the two scores. So in the example above, the shortest path goes along the pink edges because the sum of the two shortest path scores for the lower vertex is 19, which is less than the sum for the vertex settled twice.
We can follow this with a more formal proof of correctness.
Proof of Correctness
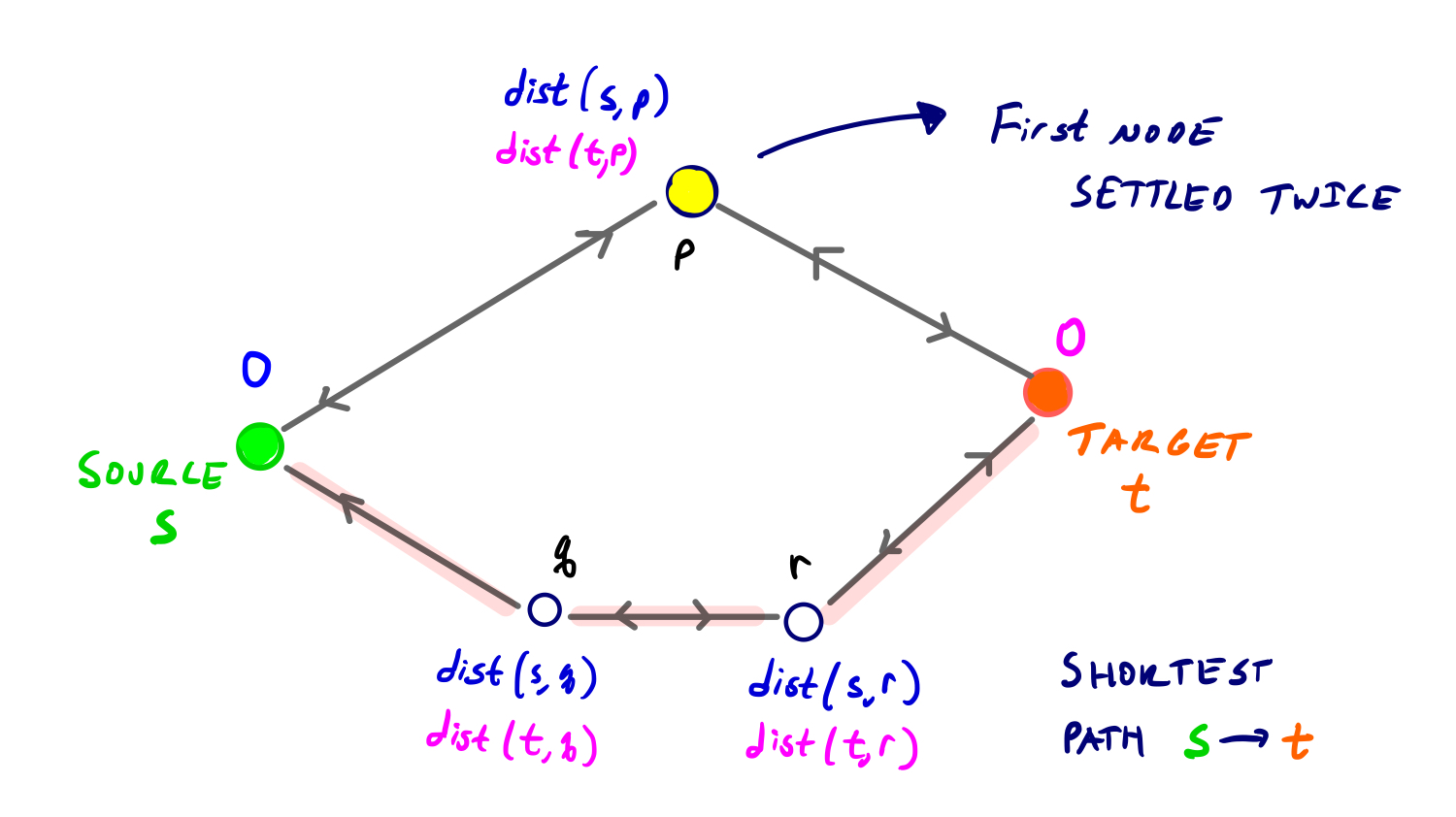
Consider the example graph above, with source and target nodes s and t, and additional nodes p, q, and r. We denote D as the length of the shortest path from s to t, and p is the first node settled twice. If dist(s, p) = dist(t, p) = D / 2, then p is on the shortest path from s to t, and we’re done.
The example above shows the second case, when the dist(s, p) and dist(t, p) are not equal to D / 2. It must be the case then, that either dist(s, p) or dist(t, p) is less than D / 2. This means that all nodes with a shortest path score of less than or equal to D / 2 (from either side) have already been settled.
We let node q and r be on the shortest path from s to t, and dist(s, q) <= D / 2 and dist(t, r) <= D / 2.
So q has been settled by s, and r has been settled by t. Then the edge qr has already been relaxed in both directions, and thus q and r both have two finite shortest path scores.
The length of the shortest path from s to t then is the smaller of dist(s, q) + dist(t, q) and dist(s, r) + dist(t, r), which in this case would be the same for both.
So, the node settled twice is not necessarily on the shortest path, but by the time the search halts, at least one node on the shortest path has a finite dist() value from both s and t.
Using Bidirectional Search
Now, given that we have this new (and at least twice as efficient) variant of Dijkstra’s algorithm, we can look at how bidirectional search can be even more useful when integrated with hierarchical approaches.