Introduction
An Overview of Speedup Approaches
Speedup techniques mostly come in two flavors: preprocessing that can augment the graph with extra information, and modifications to Dijkstra’s query method that preclude certain nodes from being settled. And most fast route-planning algorithms, like contraction hierarchies, use information gathered during preprocessing to inform the query modification.
The Preprocess, Query tradeoff
[2] and [10] provide a thorough survey on many of the speedup techniques developed in recent years. Without describing the range of approaches, we’ll just reiterate an important notion, which is the tradeoff between preprocess time, and query time.
Like we already stated, a primary objective of a route-planning algorithm is to adequately reduce the number of settled nodes to achieve as fast a query as possible.
At one extreme, we could compute the shortest path for every pair of nodes in the graph and store the results in a table during a preprocess stage. A shortest path query wouldn’t require any nodes to be settled, giving us a lower bound for the worst case query time. But of course, the preprocess stage itself would take over 6 days (see [2]).
So if we introduce a preprocess step, the objective of achieving the fastest possible query must be joined by the objective of limiting the time spent preprocessing.
And it should be clear that if we wanted the fastest preprocess step possible, we should just run an unmodified version of Dijkstra’s algorithm, which takes no preprocessing time at all. But the result then is slower queries of course. So any route planning algorithm should adequately balance the preprocess, query tradeoff.
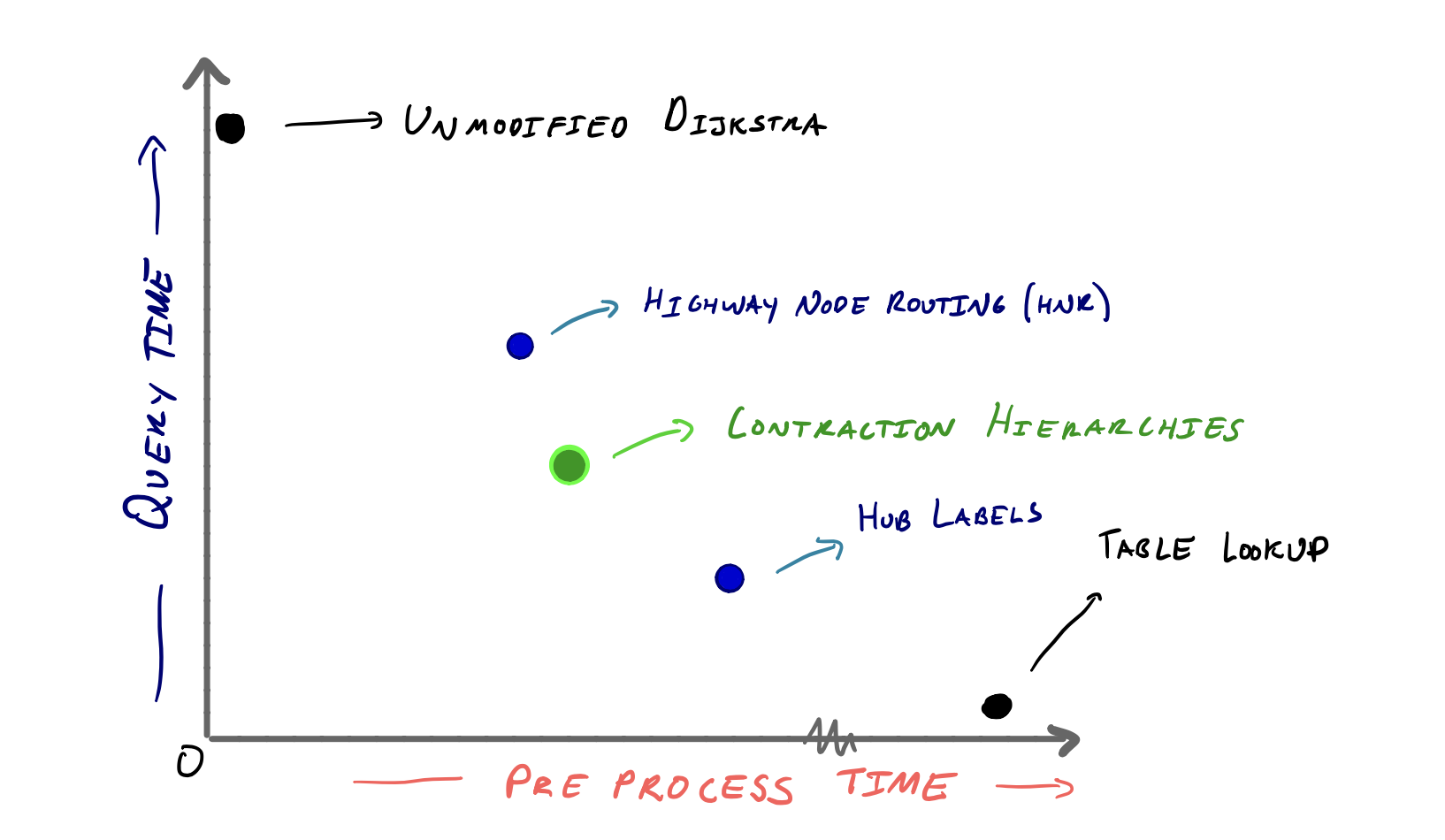
A comparison of the exact preprocess and query times across various algorithms can be found in the surveys mentioned above. But consider this graph showing where contraction hierarchies fits in according to the tradeoff. The blue dots represent other route planning algorithms which influenced or were influenced by contraction hierarchies. A well-tuned implementation of contraction hierarchies spends 5-10 minutes preprocessing (see [8]).
What Should Preprocessing Entail
So given that this tradeoff exists, we need good information to augment with, and we need to do this efficiently. A good place to start is to consider the hierarchical nature of road networks.