Introduction
Shortest Paths Using Dijkstra
Dijkstra provides us with the standard single-source shortest path (SSSP) algorithm. We briefly reintroduce the main components (which still serve as the foundation for most route planning algorithms, including contraction hierarchies).
Notation
For any two nodes u and v in the graph, we denote the length of the shortest path between the nodes as dist(u, v). We will sometimes refer to this as the shortest path score of v. This is the sum of all edge weights on that path. For an edge e from p to v we denote the weight of e as w(p, v).
We also consider the edge relaxation process: suppose we have a tentative shortest path length dist(s, v). We encounter a new edge pv with weight w(p, v). We relax pv by checking whether dist(s, v) can be improved (lowered), by using the edge pv.
In other words, if dist(s, v) > dist(s, p) + w(p, v), we reassign dist(s, v) = dist(s, p) + w(p, v). Otherwise, dist(s, v) keeps its original value. If dist(s, v) is updated, we also store the edge pv as the new predecessor path of vertex v, denoted as pred(v) = pv.
When dist(s, v) can no longer be improved by relaxing incident edges to v, we say that the node v has been settled.
Example of Relaxation
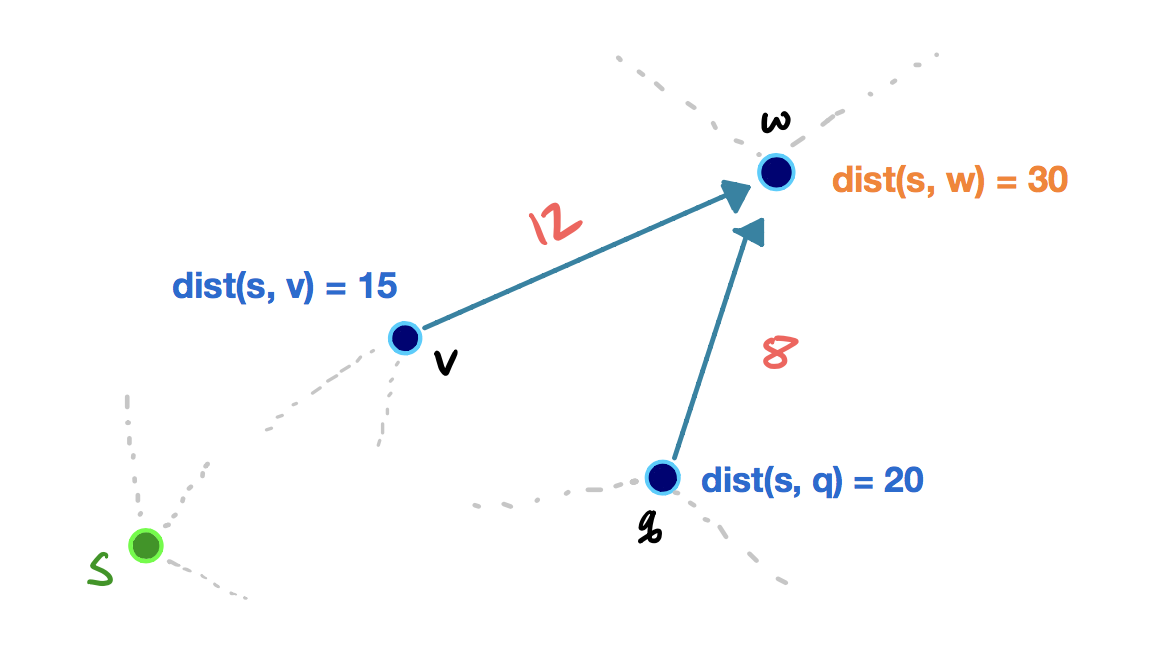
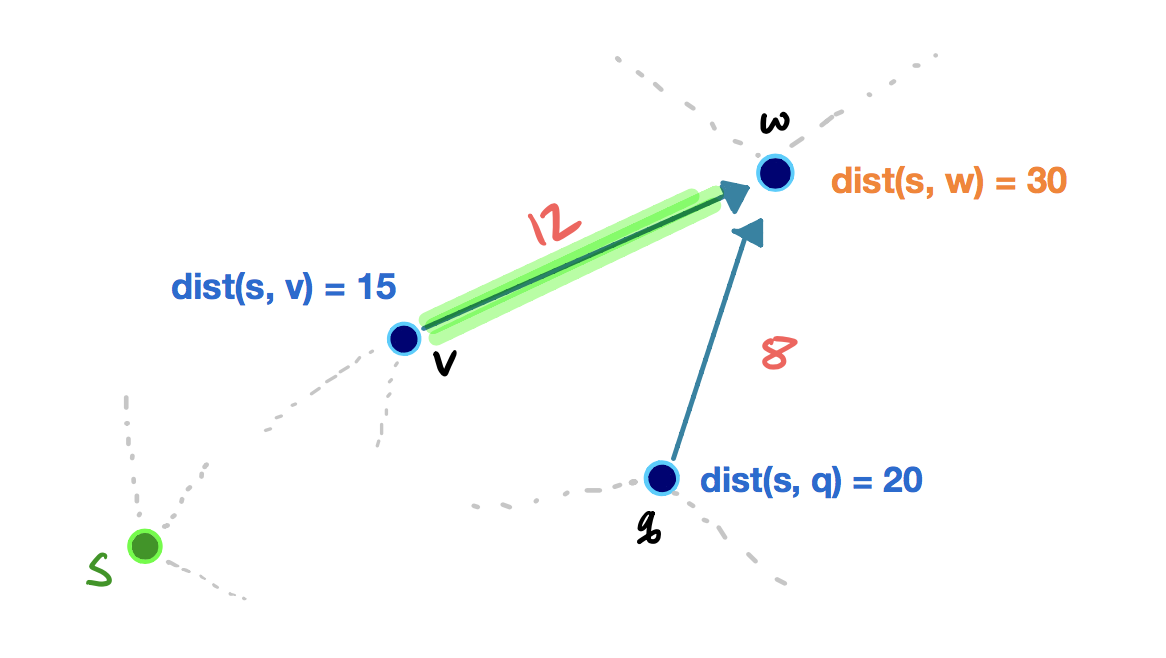
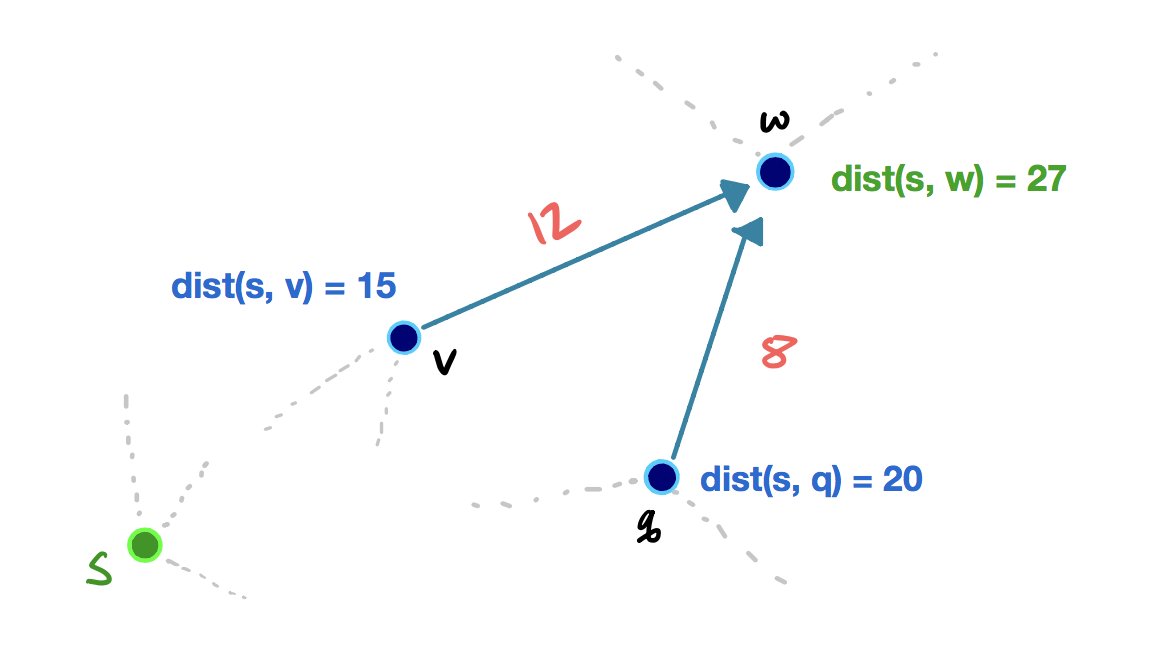
Consider this example showing an edge relaxation: (click on the arrows below to move the slides)
In the example, we have some source vertex s in a different part of the graph, and the vertices v, q, and w all have a tentative shortest path score. When we relax the edge vw, the shortest path score of w is improved from 30 to 27. If we were to relax the edge qw, the shortest path score of w wouldn’t change, since dist (s, w) < dist(s, q) + w(qw).
Dijkstra’s Approach
Given a source vertex s, Dijkstra’s algorithm uses the relaxation principle and iteratively settles the node that currently has the lowest shortest path distance from s.
For an overview:
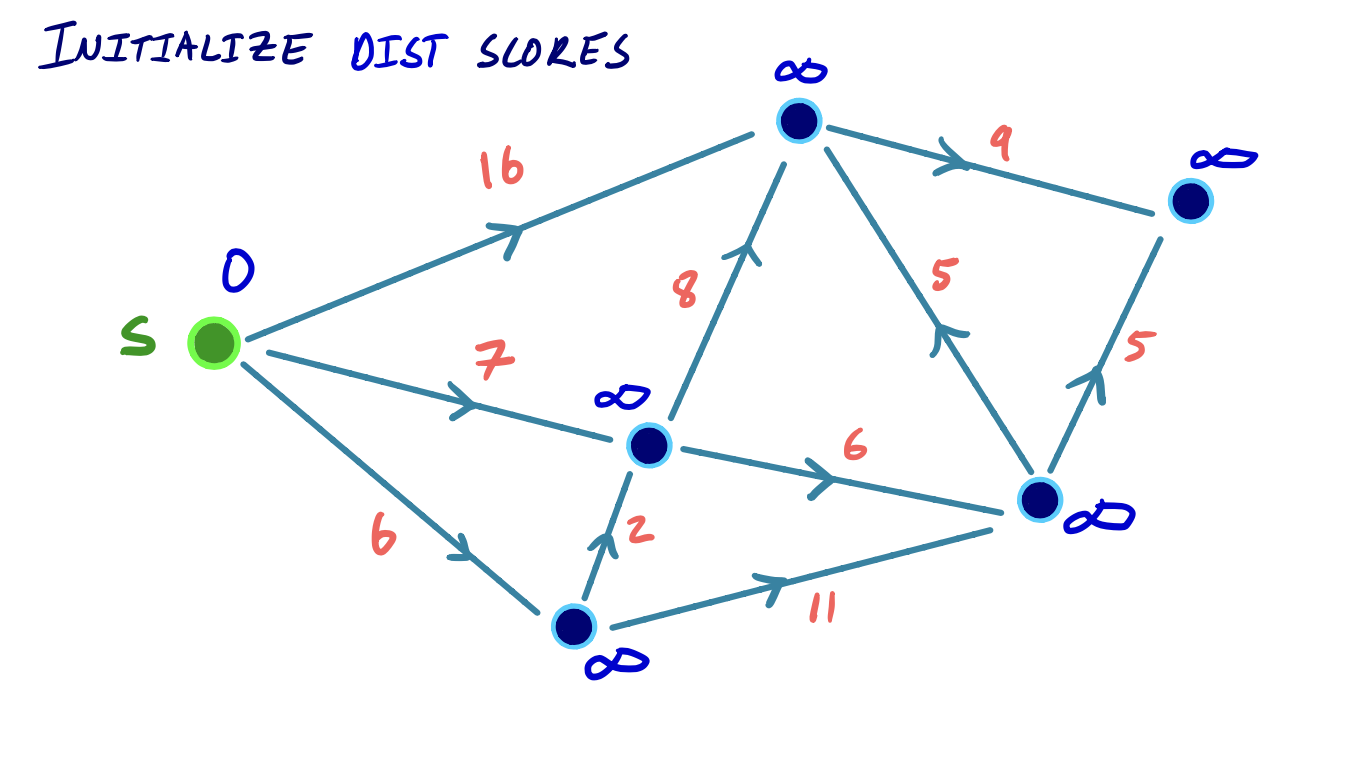
All nodes (other than the source) are initialized with a shortest path distance of infinity. The source node is given a shortest path distance of zero. All nodes are loaded into a priority queue that orders vertices by their shortest path distance from s.
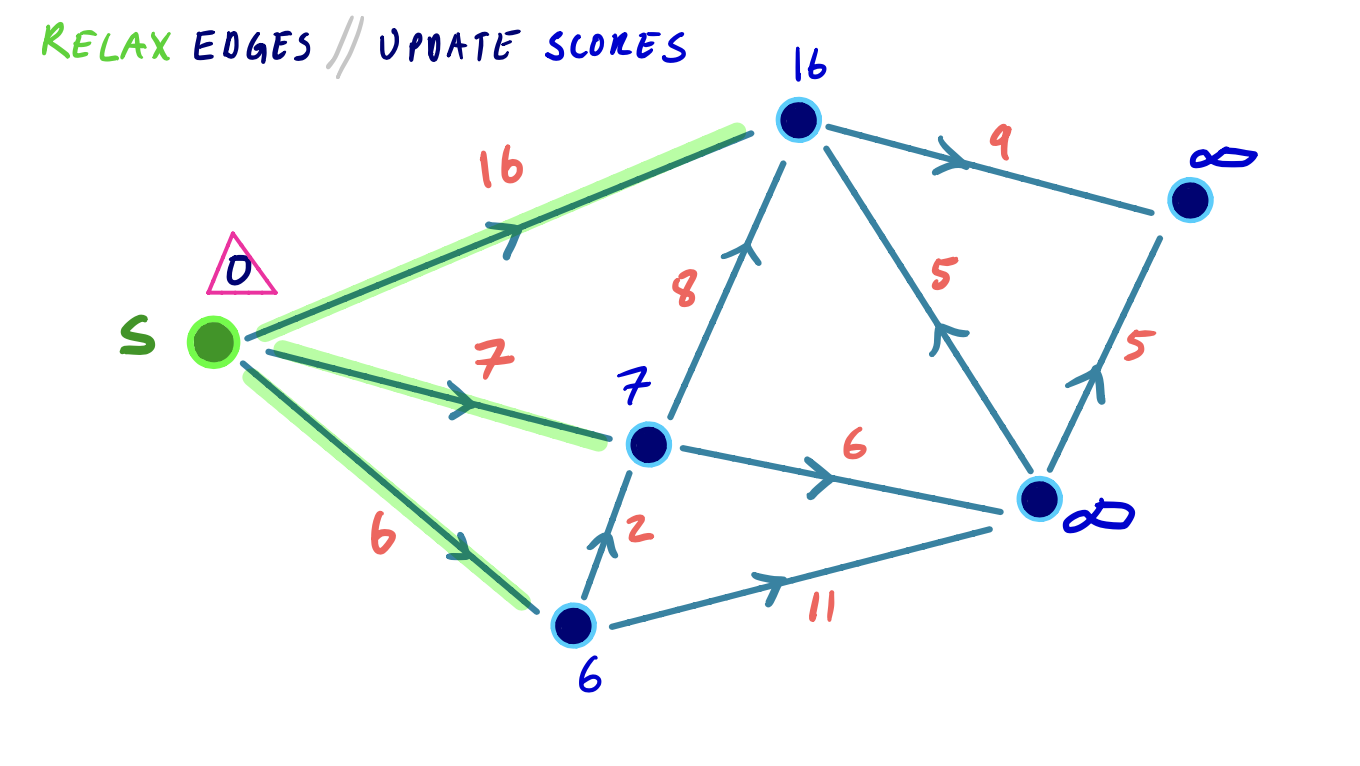
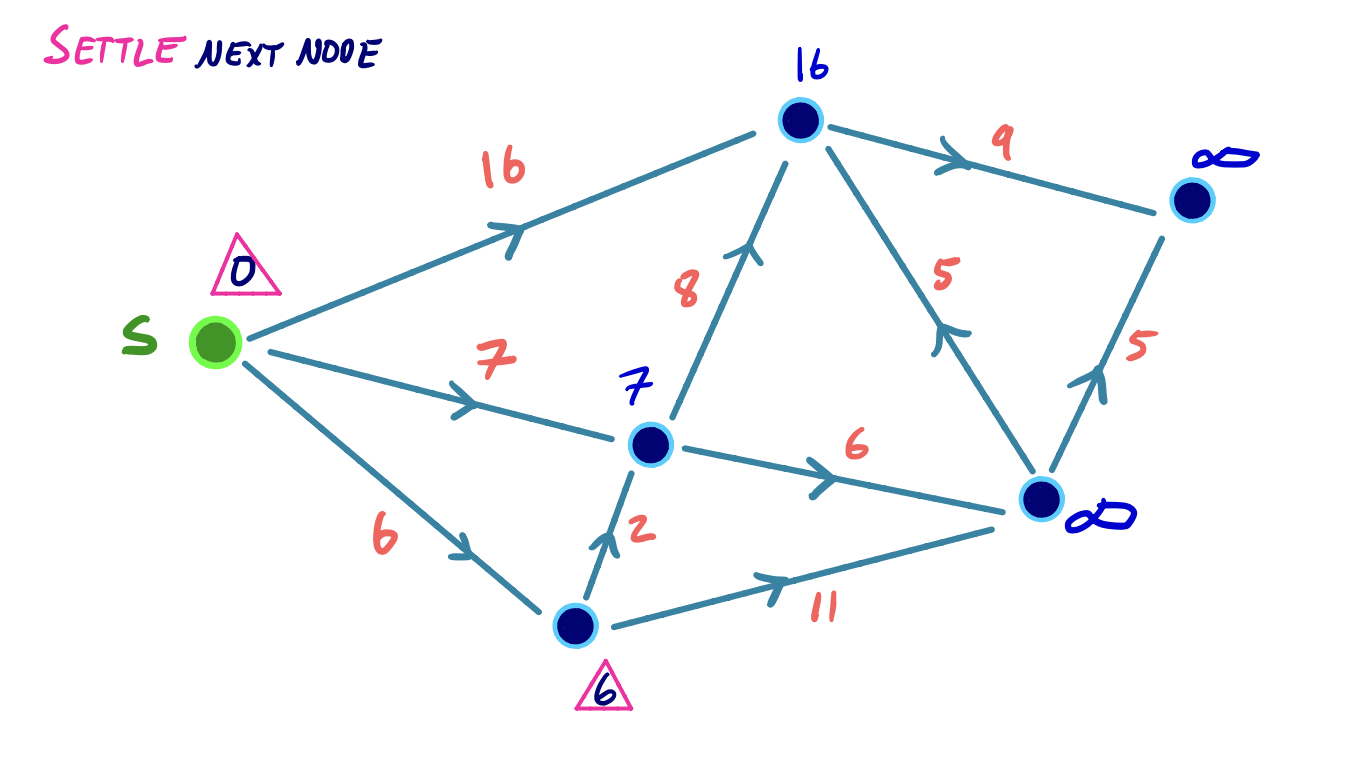
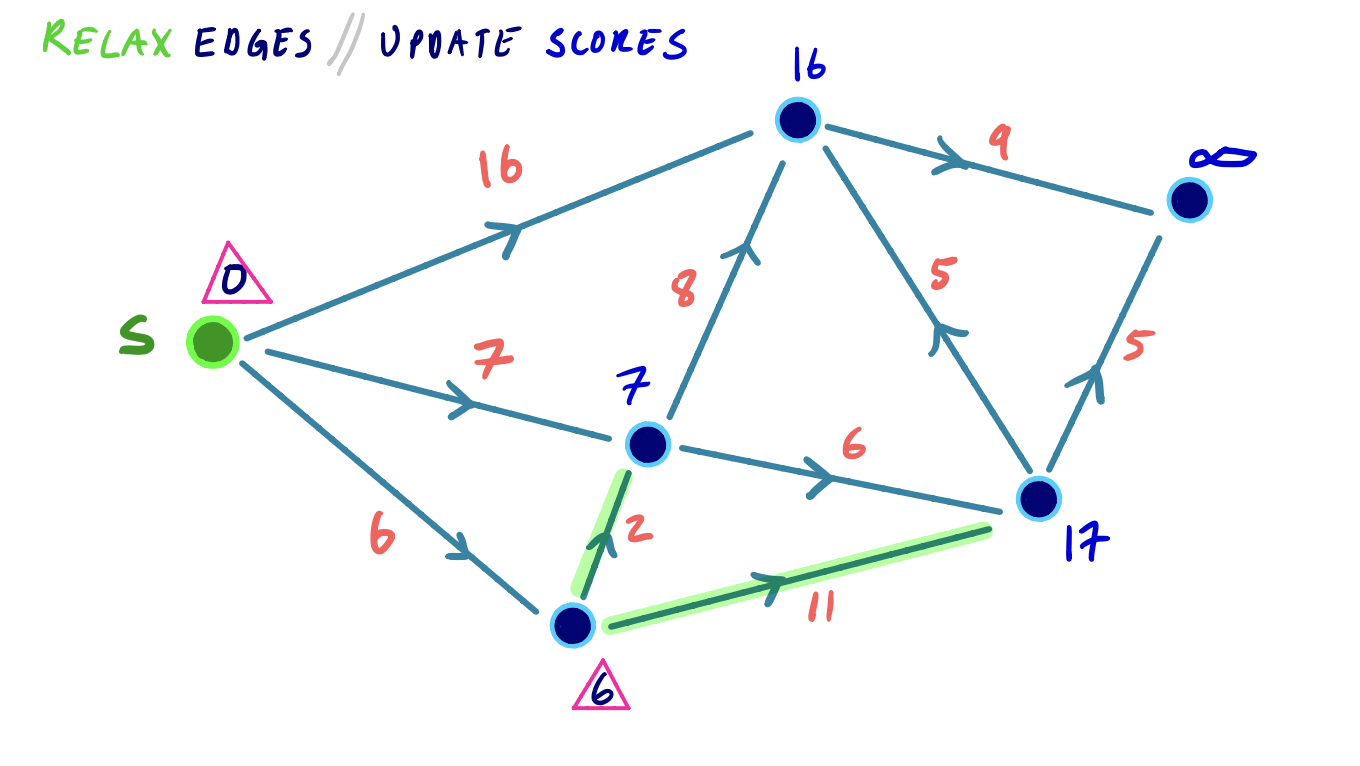
Until every node has been settled, the minimum node v is extracted, and all outgoing edges from that node are relaxed. We mark v as settled.
The priority queue is rebalanced to reflect any changes in shortest path distances resulting from the edge relaxations.
After V rounds, all nodes will be settled, and the shortest path distances from s will be calculated to every other node in the graph.
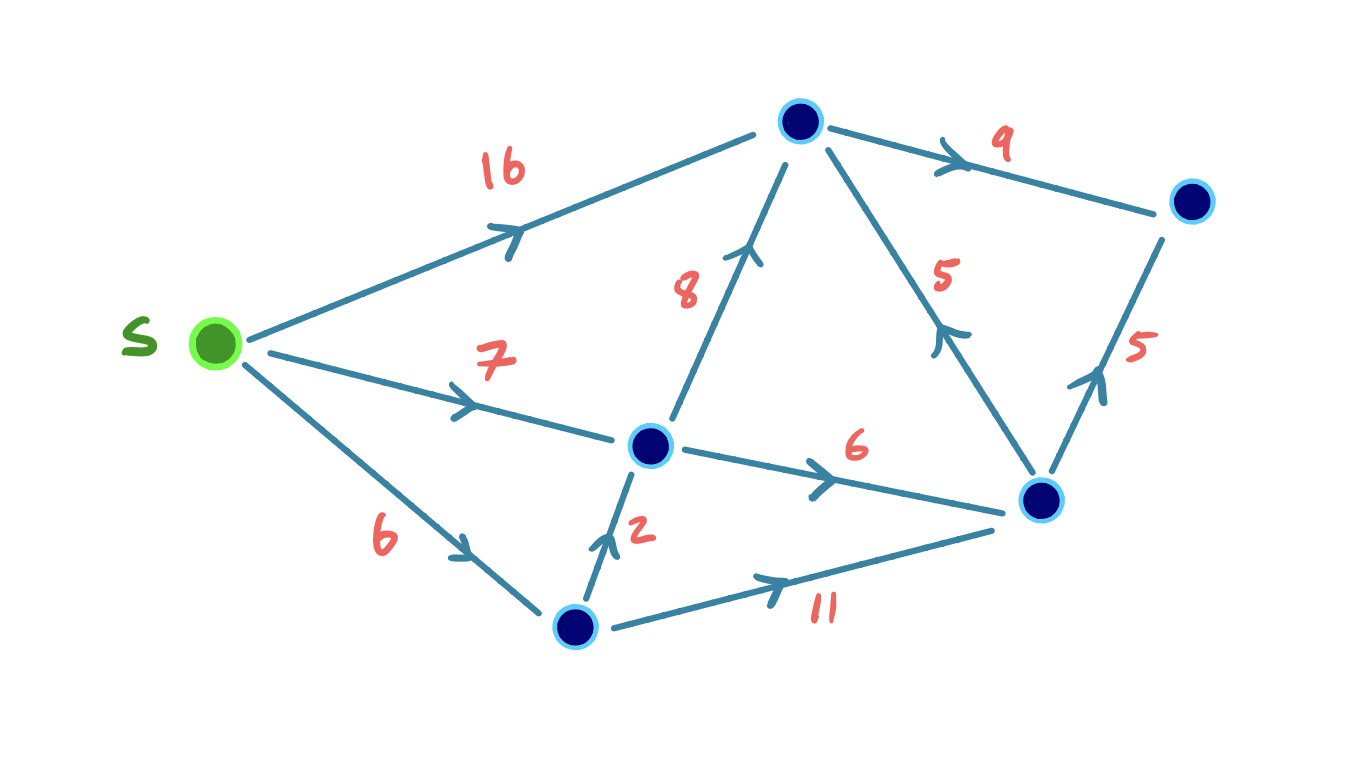
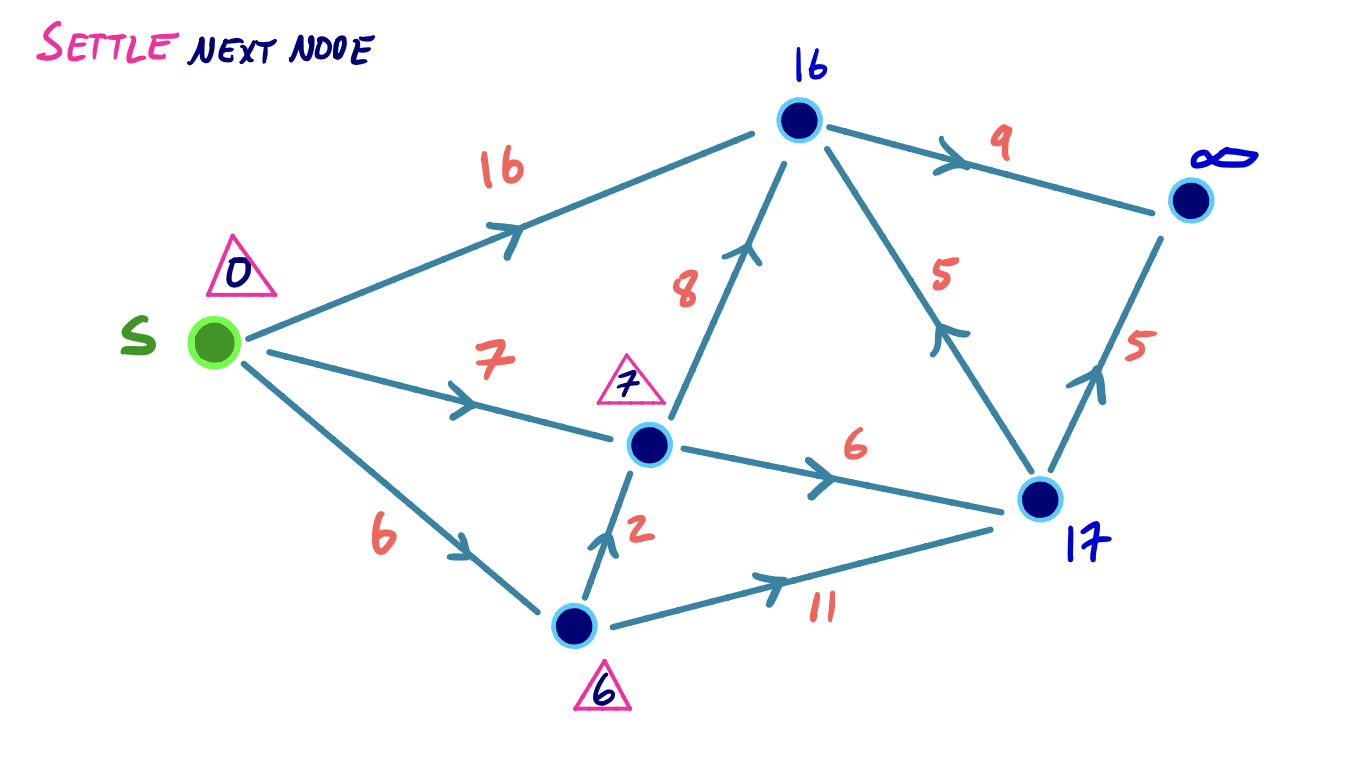
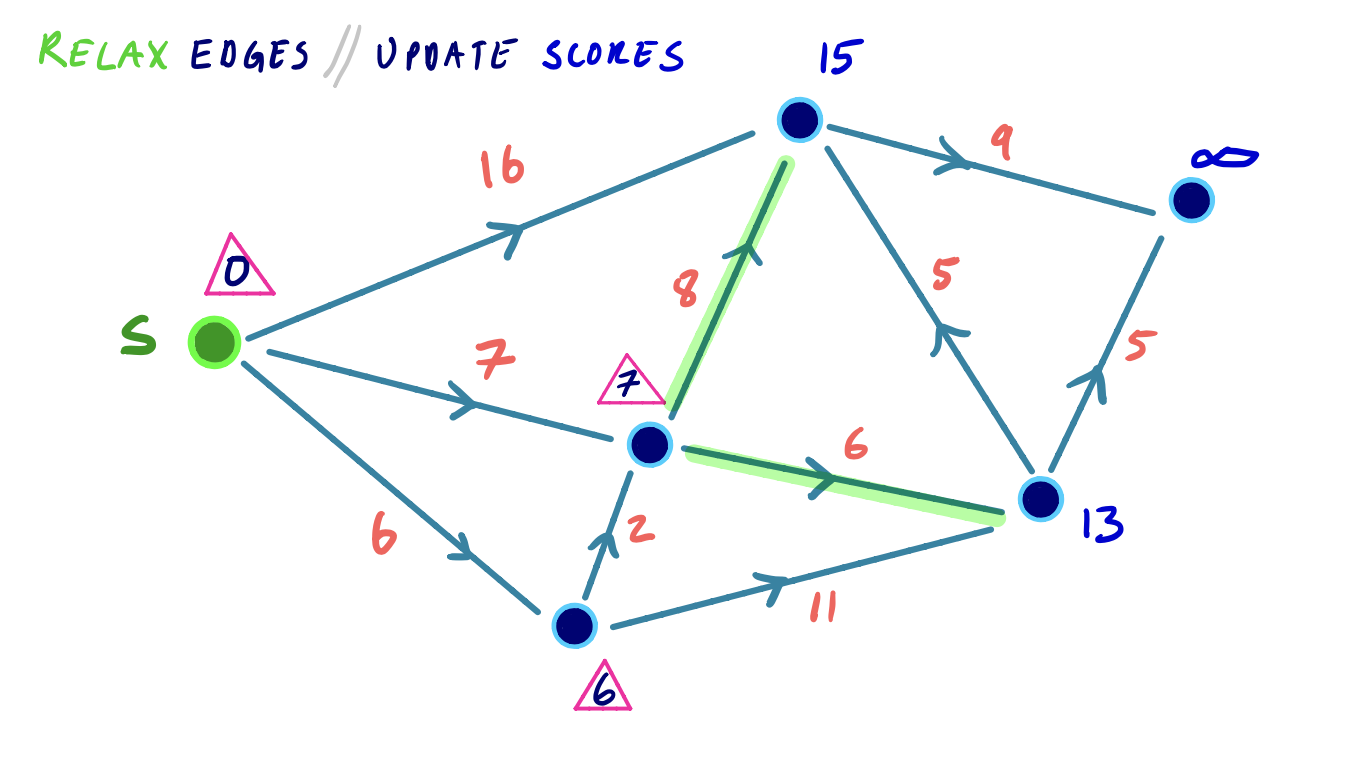
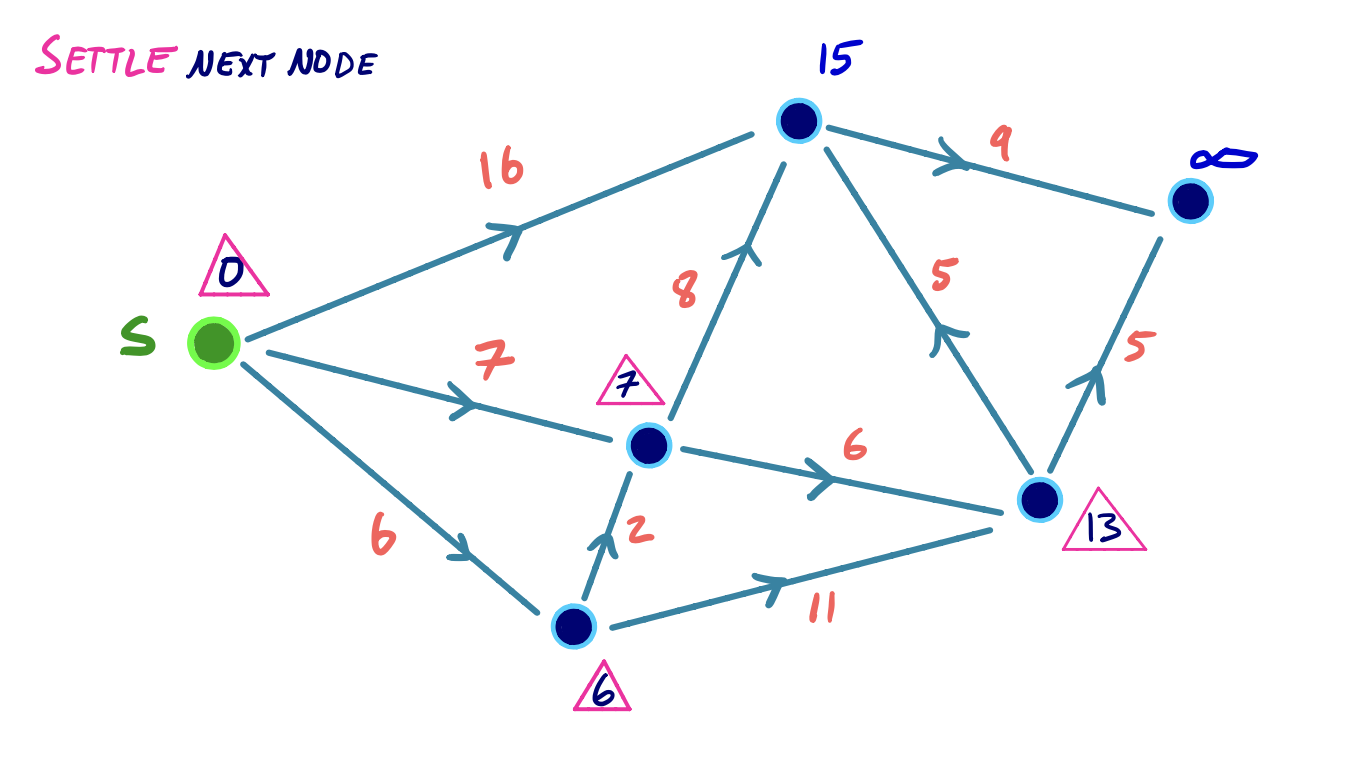
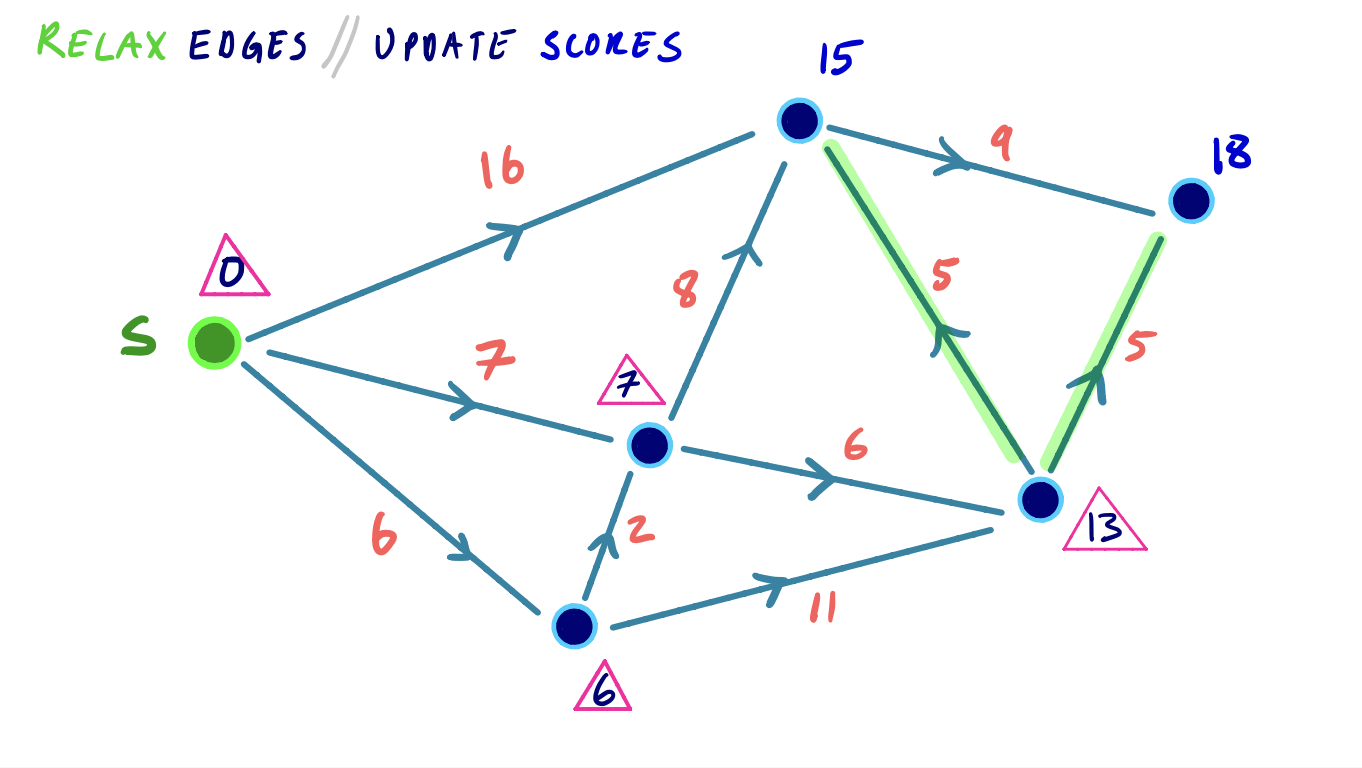
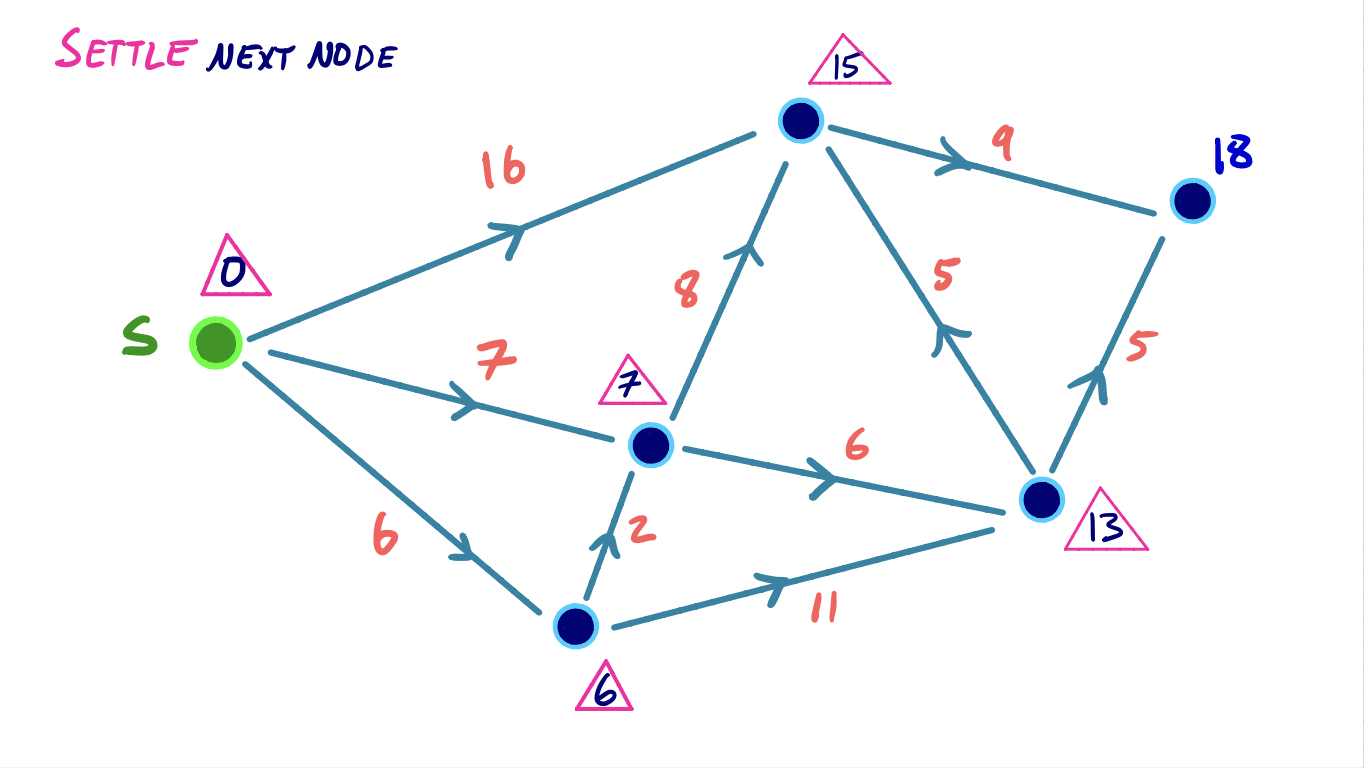
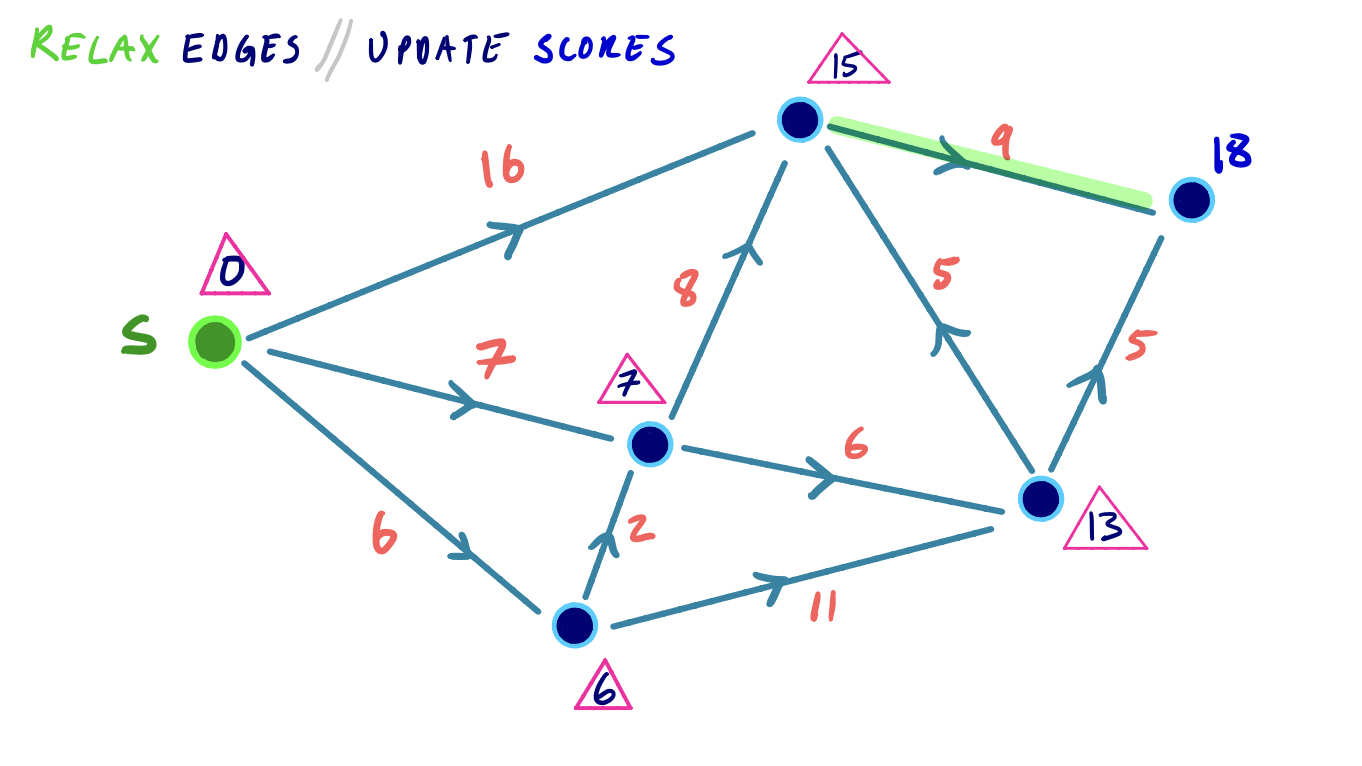
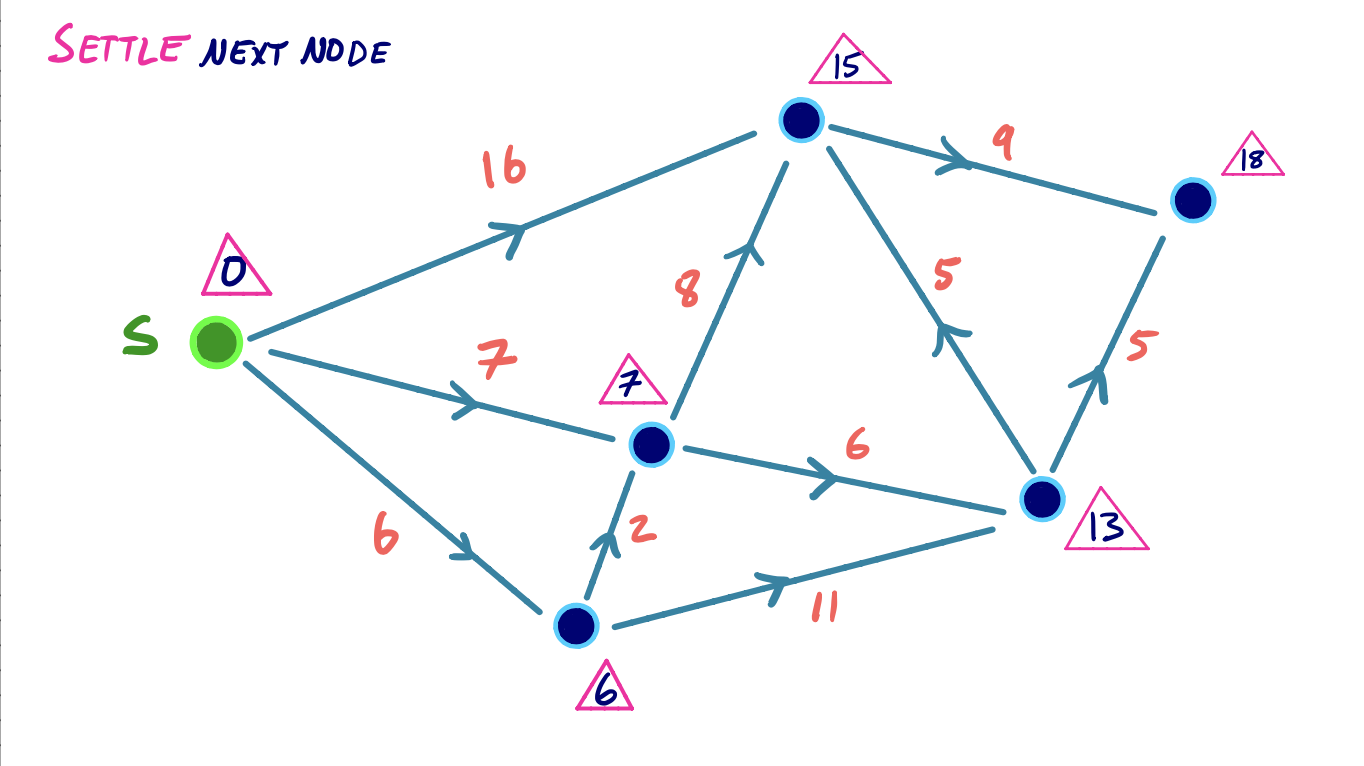
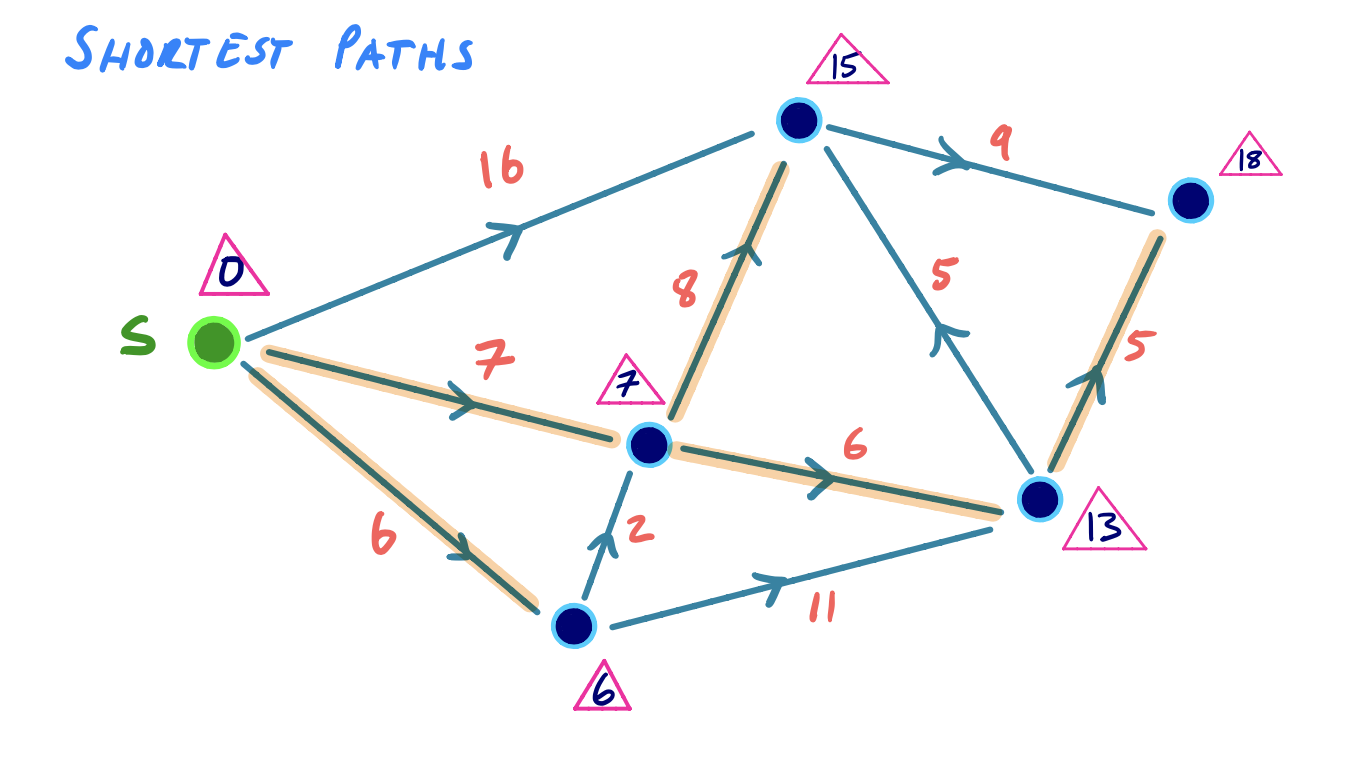
Dijkstra Example
To visualize this, we can consider the following small example, where we iteratively settle and relax outgoing edges from the node with the lowest shortest path score:
Efficiency
With Dijkstra’s algorithm, we notice that every edge in the graph is relaxed once, and every node will be settled. After every relaxation, if a shortest path distance is updated, the priority queue (implemented as a binary heap) must be rebalanced.
So to compute a complete set of single-source shortest path distances, Dijkstra’s algorithm provides a O(E log V) runtime.
Efficient for Road Networks?
But for road networks, and specifically for route-planning, we may not be interested in all shortest-path distances from a source – we’re interested in the shortest-path from one source to one target, a point-to-point query in other words.
In this case, Dijkstra’s algorithm could halt once the target node is settled. Of course, the worst-case runtime is still the same, but for some queries, unecessary work will be avoided.
So this leads to the more general question: how efficient is Dijkstra’s algorithm on road networks? Initially, it feels as if Dijkstra’s approach has a brute-force-like naivety.
The natural intution might be: why spend time settling nodes that are not in the direction of our target? And why relax edges that represent small residential streets if the shortest path to our target surely requires traveling on a highway?
For example:
Consider the example graph below, with our source at the green node and our destination the orange node:
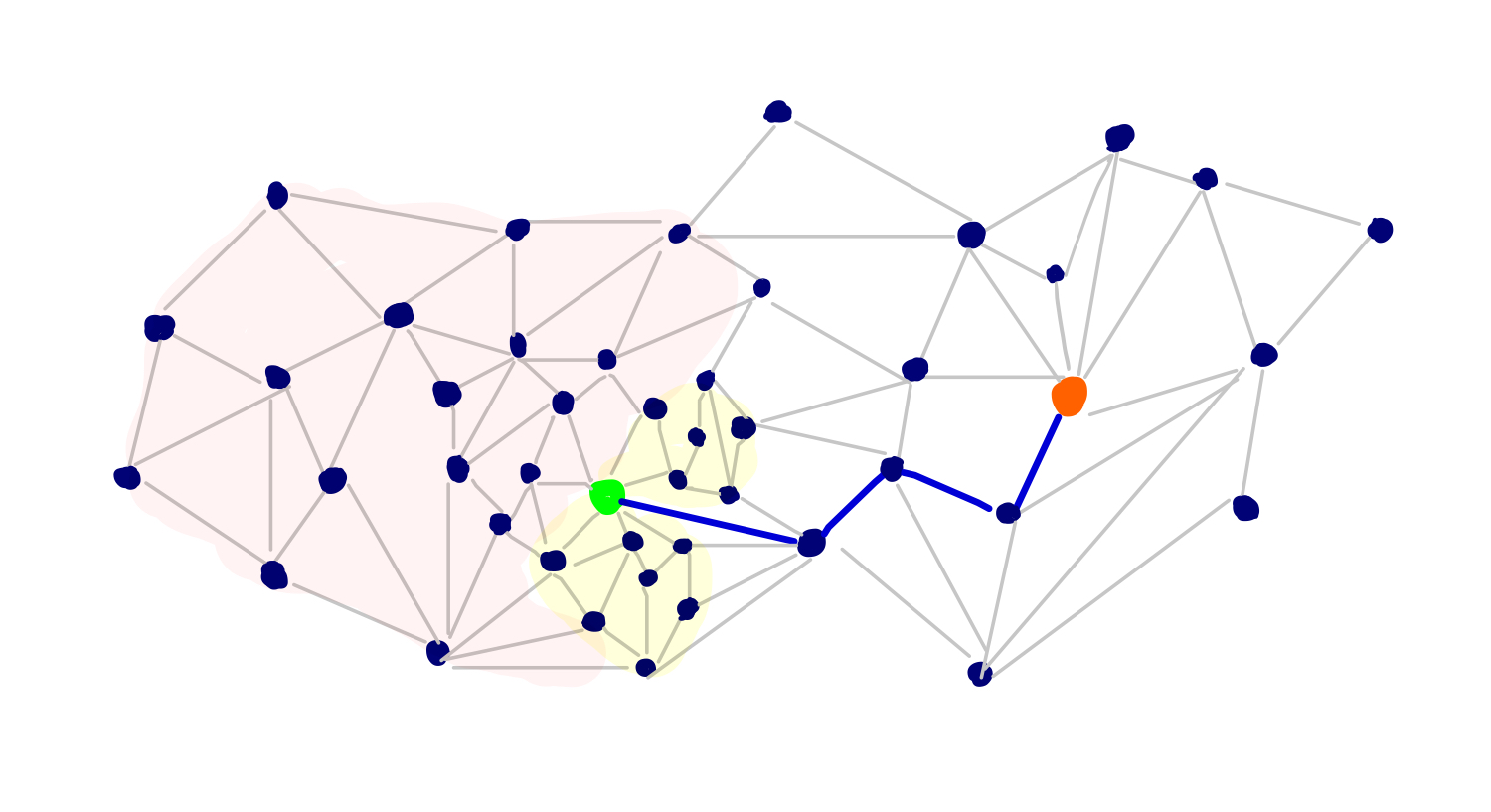
If we ran Dijstra’s algorithm from our source, we would hope to avoid settling nodes and relaxing edges in the red highlighted region given the location of our target node. But we’d also want to avoid unnecessarily searching the yellow shaded region. Here, we probably have many vertices with low dist() scores that are in the general direction of our target, but they are inconsequential to the actual shortest path.
Knowing the shortest path between two nodes makes it easy to point out unnecessarily searched portions of the graph, but the natural intuitions about the importance of certain edges over others are important for building faster algorithms.
The Need to Augment our Graphs
In its plain form however, the directed graphs used to model road networks have little awareness of these intuitions. Dijkstra’s algorithm will provide a provably correct shortest path, but as we can see, in most cases it requires processing a much larger portion of the graph than we ever need.
And this leads to the main motivation for designing more efficient route-planning algorithms:
How can information about the relative importance, location, and the type of road an edge represents be incorporated into a graph to reduce the search space of point to point queries?
In other words, if we only need to settle a small fraction of the total nodes and relax a small fraction of the total edges in a graph, and we can still return a provably correct shortest path, our point to point queries will drastically speed up. Compare this to running an unmodified version of Dijkstra’s algorithm, where we might settle every node and relax every edge in the worst case.
How Much Speedup is Possible?
As a sneak-preview to just how much speedup is possible with an algorithm like contraction hierarchies, look at some benchmark results from [2].
A series of shortest path queries were made using various algorithms, and the average number of vertices scanned (on the receiving end of an edge relaxation) and the average time per query were recorded. The tests were run on a Western Europe road network graph:
| Algorithm | # of Scanned Vertices | Query Time (microseconds) |
|---|---|---|
| Dijkstra | 9326696 | 2195080 (~ 2 seconds) |
| Contraction Hierarchies | 280 | 110 |
Clearly, it is possible to engineer techniques that only need to process a tiny fraction of the original graph during queries.
But given what we know about Dijkstra’s algorithm, we’ll need to augment our graph with information that would allow us to reduce our search space.
So we continue by discussing a few categories of speedup techniques and then start laying the foundation for contraction hierarchies.