Core Components of CH
Query Correctness
Here we show that the query algorithm described in the previous section is correct on the G* graph produced from any node contraction order. Moreover, it will follow that shortest paths in G* are also shortest paths in the original graph G.
Note that although we already proved that a general bidirectional Dijkstra query is correct, we have to do a little more work to show that the CH modified query also holds.
Our Notation
First we should restate some of the notation that was introduced in earlier sections:
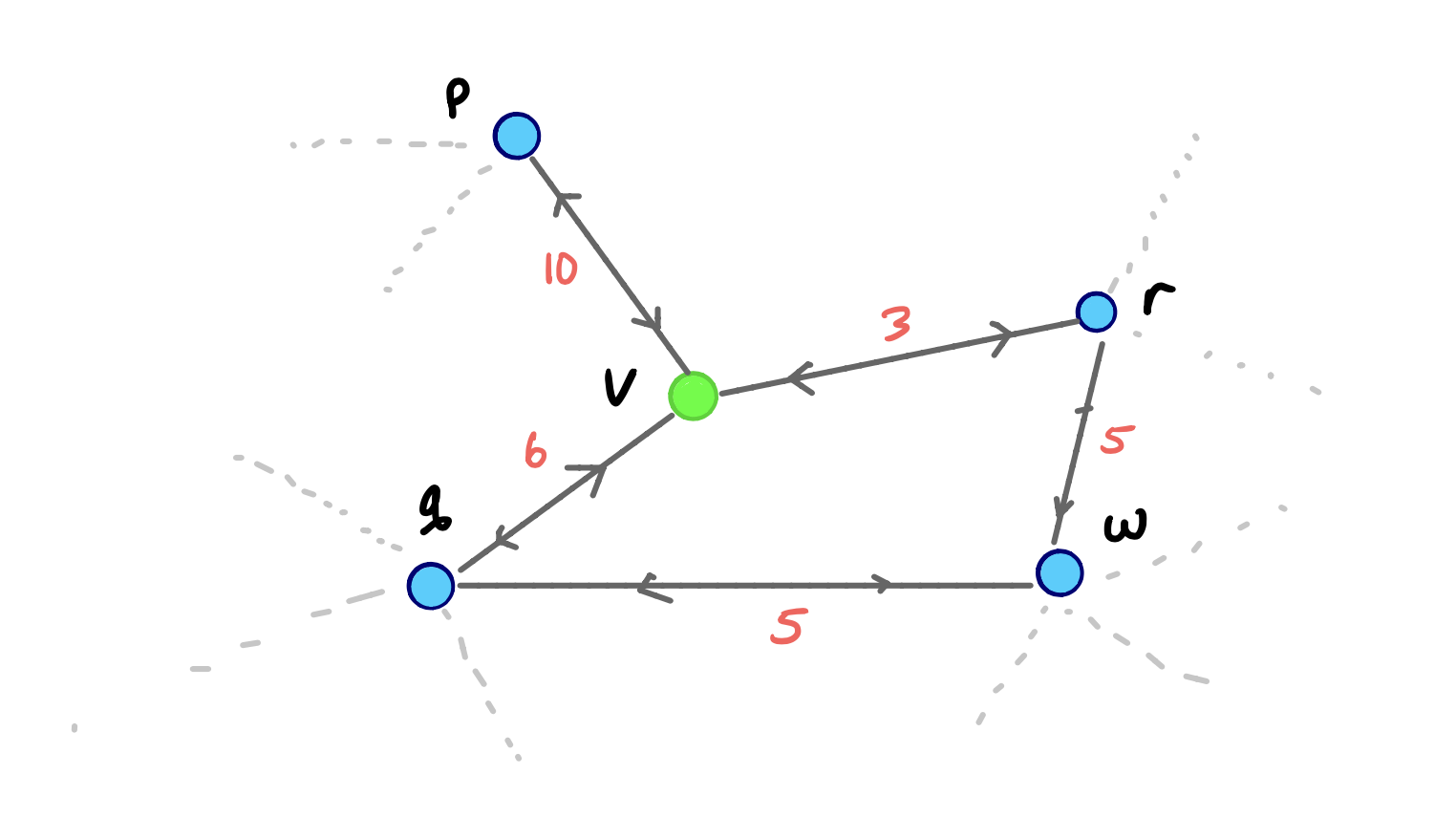
We have some node ordering O = {v1, … , vn} for every v in V.
We denote G0 as the original graph G. And Gi is the subgraph induced by contracting node vi in Gi-1.
Gi then does not contain vi or its adjacent edges, but it does contain any shortcut edges added after vi was contracted. So Gi contains n-i nodes.
We denote the shortest path between two nodes u, v in Gi as disti(u, v).
G* is the overlay graph containing all nodes and all edges in G, and all shortcut edges added in any {G1, … , Gn-1}.
The Contraction of All Nodes Preserves Shortest Paths
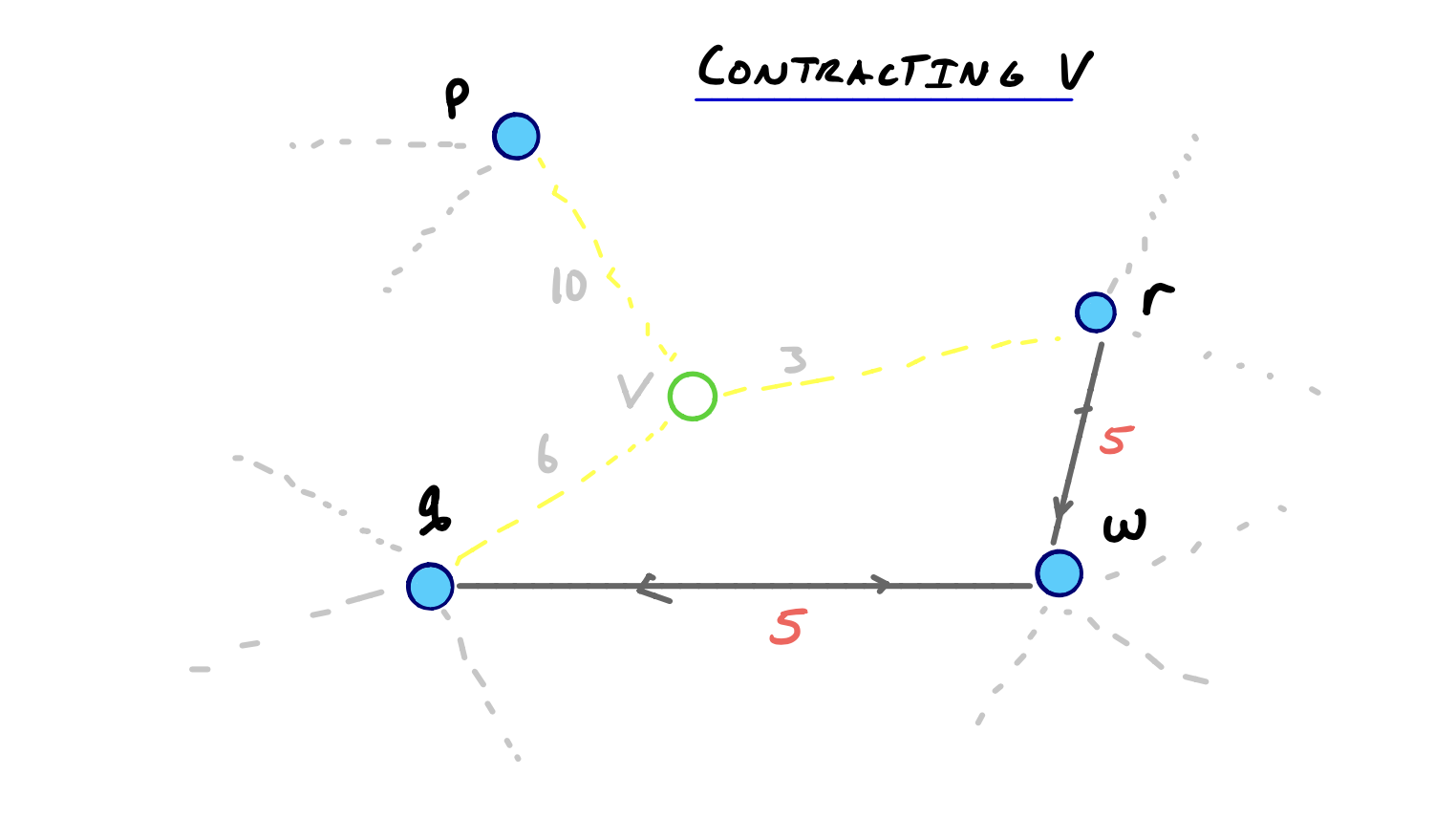
We state Lemma 1, which tells us that the shortest path length between two nodes is the same before and after a given round of contraction.
Formally:
For all nodes s and t in Gi, disti(s, t) = disti-1(s, t) for i in [1, n].
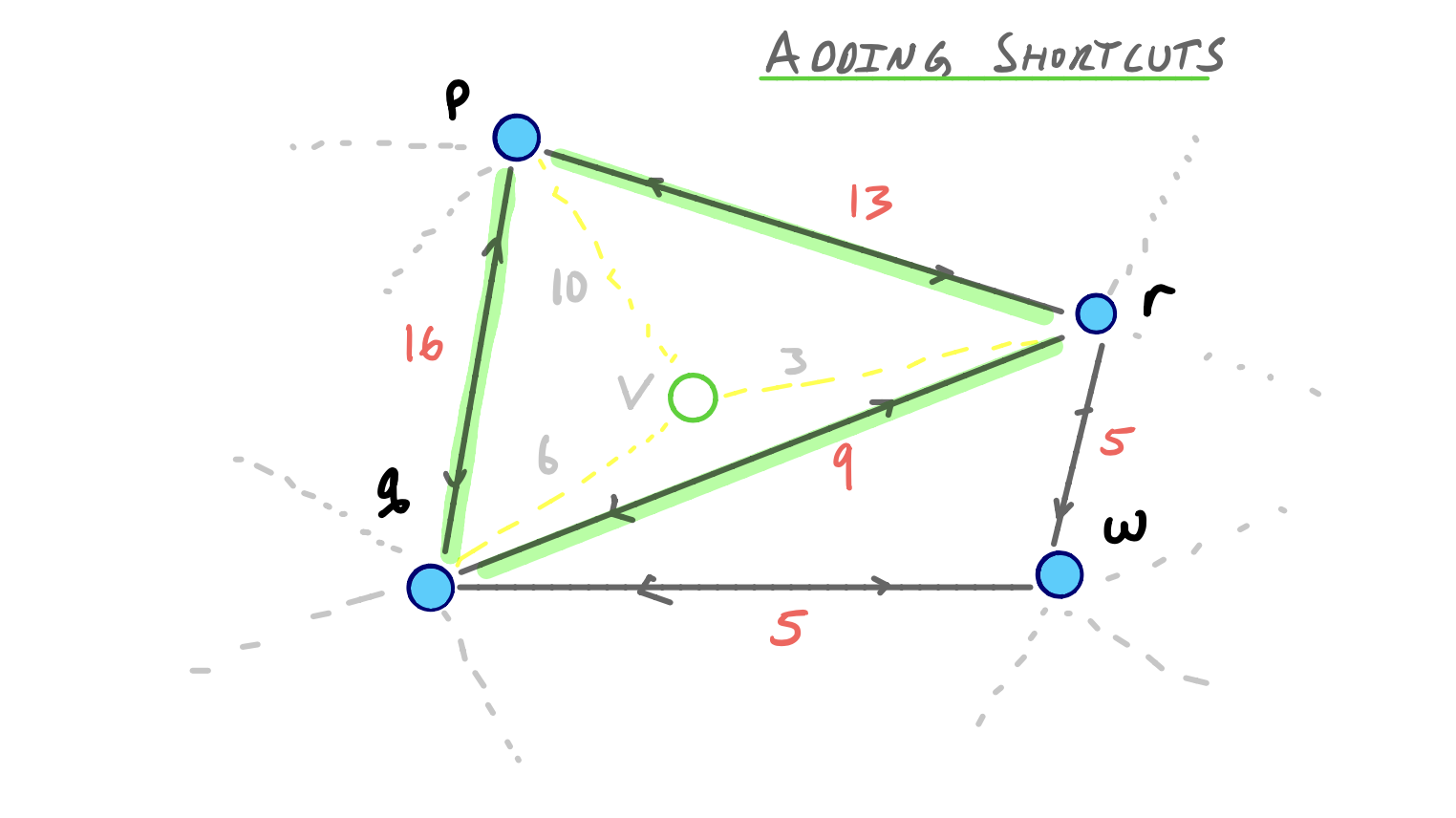
If we have a shortest path P from s to t in Gi, either P contains a shortcut added after contracting vi or it doesn’t. If it doesn’t, then P also must exist in Gi-1. If P does have a shortcut that was added in this round of contraction, consider that the shortcut edge is uw, and u and w are both neighbors of vi. Then there is also some path <uviw> in Gi-1 with the same cost as uw, because that’s why we added the shortcut in the first place. And therefore disti-1(s, t) <= disti(s, t).
And similarly, consider now a shortest path P from s to t in Gi-1. Either P has edges that go through vi (the node that will be contracted in the next round), or it doesn’t. If it doesn’t, then P is the same in Gi-1 as it is in Gi. If P does contain edges through vi, then in Gi we’ll be adding a shortcut edge with the same weight. So disti(s, t) <= disti-1(s, t).
So disti(s, t) = disti-1(s, t).
This result is more or less obvious, but if you want a visual example to prove this lemma for yourself, you can reconsider our original contraction example:
The Query is Correct
Now, we’ll use this first lemma to prove that, as we said in the previous section:
dist(s, t) = min{ dist(s, v) + dist(v, t)} over all v in L
where L is the set of all nodes settled in both searches on the G*U graph from s and t.
We also can reiterate that when considering symmetric graphs (every edge goes both directions), a forward search on G*U is identical to a backward search on G*D. So wlog, we consider that our two searches from s and t run on G*U, as we described in the previous section.
Now, we consider the shortest path P from s to t in G. We define vertex m as the node with the highest order (i.e. contracted later than others) on the path P.
We say that there is a prefix path in P that contains a set of nodes {v0, v1, … , vk} such that vi-1 < vi, where the < symbol (as said before) indicates that vi-1 was contracted before vi. In other words, the prefix path contains the longest subsequence of nodes on the portion of the shortest path from s to m such that each node has a lower contraction order than the next.
We can use the following illustration to visualize m and the prefix path. We only consider the search starting from s for now, but this argument is completely analogous to the search starting from t:
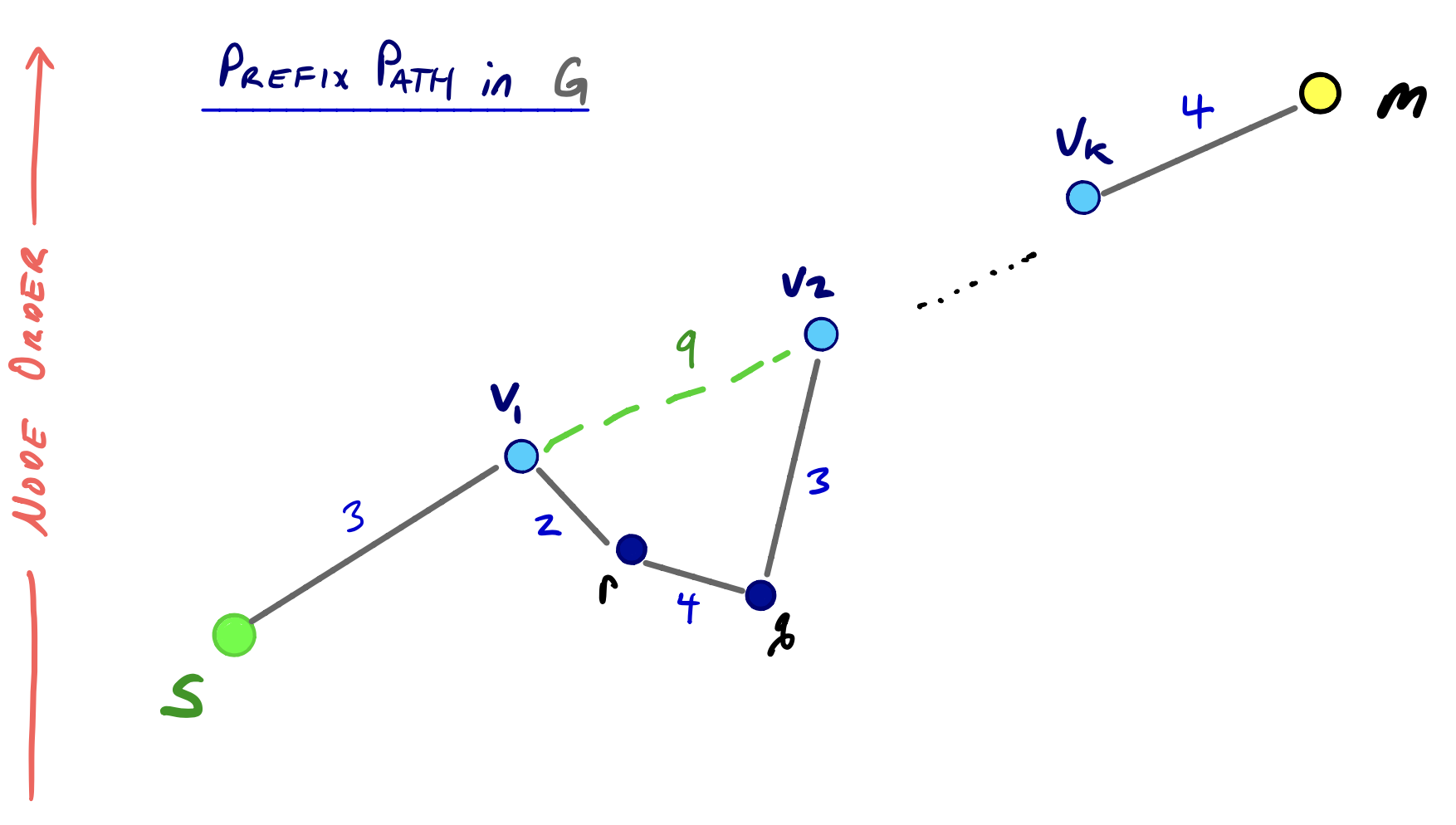
Because we defined our path P as existing in the original graph G, we also see that P can have edges between two nodes like v1 and r and r and q, where v1 > r > q. There is nothing from precluding this edge from belonging to P.
However, we can show that there must exist either shortcut edges or original edges in G* between all nodes in the prefix path. (The shortcut edges that would appear in G* are dotted green in the illustration above). And moreover, these shortcuts have weights that preserve the cost of edges along the actual shortest path.
For example, consider the graph G’ right before node v1 is contracted. Then lower-ordered vertices like r and q and their incident edges aren’t in G’, since by definition, those vertices were already contracted in earlier rounds.
But by Lemma 1, we must have a path from v1 to v2 that preserves the cost of the shortest path between those two nodes. And if that edge is not an original edge in G, then it must have already been added as a shortcut and appear in G'.
And if we continue this argument further up the prefix path, we can conclude that all edges between nodes in the prefix path must exist in G*. If we tried to give a counter argument that there exists some intermediary node v’ such that v’ > vi and v’ lies on the path between vi and vi+1, then by definition v’ itself would be on the prefix path.
So this proves that the shortest path distance from s to m in G*U is equal to the shortest path distance from s to m in the original graph G. And like we said earlier, because our backward search on G*D from t is equivalent to the forward search on G*U from t, the same argument holds for the path from t to m.
And because m is on the shortest path from s to t in G, m must have been among the nodes settled by both searches during the bidirectional query on G*U. So by taking the minimum sum of the two shortest path scores among all the nodes settled by both searches (the set L), we will find the sum of the two scores at node m. And whether or not the paths from s to m and t to m contain shortcut edges in G*, we know that dist(s, t) is the same in G* as it is in G, since by Lemma 1, adding shortcuts through contraction preserves shortest path lengths.
It then only follows to backtrack the parent edge pointers in G in both directions from m as shown in the previous section.
For more detailed proofs of query correctness see [9] and [2].
Node Ordering
So our query is correct for any contraction order, but this doesn’t necessarily mean that all node orderings lead to the same query performance. So we continue to understand how node orderings are determined.